2023年四川省成都市武侯区西川实验学校中考数学诊断试卷

一.选择题（每题4分，共32分）

• 1．下列各数中，无理数是（　　）

  A． π 2	B． 22 7
  C． 4	D．0.101001000
  组卷：128引用：4难度：0.9

  解析

• 2．下列立体图形 ①长方体②圆锥③圆柱④球中，左视图可能是长方形的有（　　）

  A．①

  B．①②

  C．①③

  D．①④
  组卷：386引用：3难度：0.7

  解析

• 3．据2022年北京冬奥会新闻发言人透露，中国大陆地区约316000000人次收看了冬奥会的开幕式．数据316000000用科学记数法表示为（　　）

  A．316×106

  B．31.6×107

  C．3.16×108

  D．3.16×109
  组卷：137引用：3难度：0.9

  解析

• 4．下列不等式一定成立的是（　　）

  A．4a＞3a

  B．-b＞-2b

  C．3-x＜4-x

  D． 3 c ＞ 2 c
  组卷：489引用：13难度：0.9

  解析

• 5．若点A（a,a-1）在x轴上，则点B（a+1，a-2）在第（　　）象限．

  A．一

  B．二

  C．三

  D．四
  组卷：446引用：5难度：0.7

  解析

• 6．如果一个三角形的两边长分别为5cm、10cm,那么这个三角形的第三边的长可以是（　　）

  A．3cm

  B．5cm

  C．10cm

  D．16cm
  组卷：603引用：7难度：0.8

  解析

• 7．顺次联结一个四边形各边中点，所得的四边形是矩形，那么这个四边形是（　　）

  A．矩形

  B．正方形

  C．菱形

  D．对角线互相垂直的四边形
  组卷：129引用：2难度：0.5

  解析

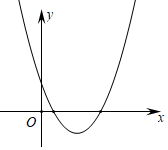• 8．如果二次函数y=（x-m）²+n的图象如图所示，那么一次函数y=mx+n的图象经过（　　）

  A．第一、二、三象限	B．第一、三、四象限
  C．第一、二、四象限	D．第二、三、四象限
  组卷：1002引用：4难度：0.6

  解析

二.解答题（共30分）

• 25．定义：将二次函数l的图象沿x轴向右平移t,再沿x轴翻折，得到新函数l′的图象，则称函数l′是函数l的“t值衍生抛物线”．已知l：y=x²-2x-3．
  
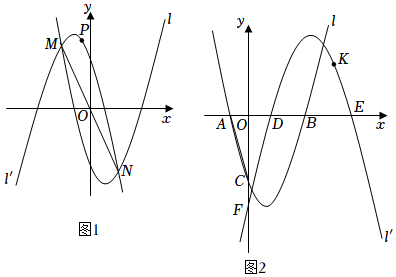
  （1）当t=-2时，
  ①求衍生抛物线l′的函数解析式；
  ②如图1，函数l与l'的图象交于M（-

  3

  ，n），N（m,-2

  3

  ）两点，连接MN．点P为抛物线l′上一点，且位于线段MN上方，过点P作PQ∥y轴，交MN于点Q，交抛物线l于点G，求S_△QNG与S_△PNG存在的数量关系．
  （2）当t=2时，如图2，函数l与x轴交于A，B两点，与y轴交于点C，连接AC．函数l′与x轴交于D，E两点，与y轴交于点F．点K在抛物线l′上，且∠EFK=∠OCA．请直接写出点K的横坐标．
  组卷：980引用：3难度：0.2

  解析

• 26．如图，已知矩形ABCD中，E是边AD上一点，将△BDE沿BE折叠得到△BFE，连接DF．
  （1）如图1，BF落在直线BA上时，求证△DFA∽△BEA；
  （2）如图2，当

  AD

  AB

  =

  2

  时，BF与边AD相交时，在BE上取一点G，使∠BAG=∠DAF，AG与BF
  交于点H，
  ①求

  AF

  AG

  的值；
  ②当E是AD的中点时，若FD•FH=15，求AG的长．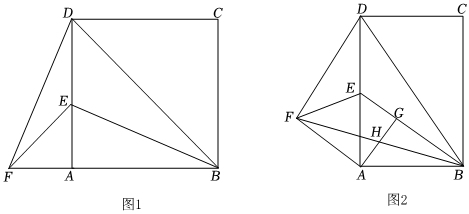
  
  组卷：345引用：1难度：0.1

  解析