2022-2023学年北京师大附属实验中学高二(下)期中物理试卷
发布:2024/10/2 15:0:2
一、单项选择题(本题共10小题,在每小题给出的四个选项中,只有一个选项最符合题意。每小题2分,共20分)
-
1.体操运动员在落地时总要屈腿,这样做可以( )
组卷:84引用:8难度:0.8 -
2.如左图,三只狗拉动雪橇在水平雪地上匀速前进,简化示意图为右图,头狗在中间沿y轴引领方向,两侧狗拉力F2与F3的合力大小不变方向始终沿y轴,设雪橇受到的摩擦力大小恒为f,则( )
 组卷:160引用:4难度:0.7
组卷:160引用:4难度:0.7 -
 3.一列简谐横波某时刻的波形如图所示,比较介质中的三个质点a、b、c,则( )组卷:1688引用:26难度:0.8
3.一列简谐横波某时刻的波形如图所示,比较介质中的三个质点a、b、c,则( )组卷:1688引用:26难度:0.8 -
 4.航天员在地面模拟失重训练的一种方式是在水下进行(如图)。航天员需要穿水槽训练航天服浸没在水中,通过配重使其在水中受到的浮力和重力大小相等,假设其总质量为m,训练空间的重力加速度为g且不变,在某次出舱作业过程中,给自己一个初速度后竖直向上匀速漂浮,下列说法正确的是( )组卷:75引用:2难度:0.8
4.航天员在地面模拟失重训练的一种方式是在水下进行(如图)。航天员需要穿水槽训练航天服浸没在水中,通过配重使其在水中受到的浮力和重力大小相等,假设其总质量为m,训练空间的重力加速度为g且不变,在某次出舱作业过程中,给自己一个初速度后竖直向上匀速漂浮,下列说法正确的是( )组卷:75引用:2难度:0.8 -
 5.高度差一定的两点间可以搭建无数条光滑的曲线轨道,让相同小球从起点端静止向下滑落,其中有一条曲线轨道的小球是最先到达终点端,这条曲线我们称之为最速降线。如图所示,6个轨道起始端和终点端高度差相同,其中轨道3满足最速降线,6个相同的小球同时从起始端静止释放最后都到达终点端的整个过程中,不计一切阻力,下列说法正确的是( )组卷:88引用:2难度:0.5
5.高度差一定的两点间可以搭建无数条光滑的曲线轨道,让相同小球从起点端静止向下滑落,其中有一条曲线轨道的小球是最先到达终点端,这条曲线我们称之为最速降线。如图所示,6个轨道起始端和终点端高度差相同,其中轨道3满足最速降线,6个相同的小球同时从起始端静止释放最后都到达终点端的整个过程中,不计一切阻力,下列说法正确的是( )组卷:88引用:2难度:0.5 -
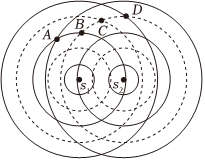 6.如图所示,s1,s2是同频率同步调的两个水波波源,实线代表波峰,虚线代表波谷,A、B、C、D四个点为相应线条的交点,下列说法中正确的是( )组卷:323引用:2难度:0.6
6.如图所示,s1,s2是同频率同步调的两个水波波源,实线代表波峰,虚线代表波谷,A、B、C、D四个点为相应线条的交点,下列说法中正确的是( )组卷:323引用:2难度:0.6 -
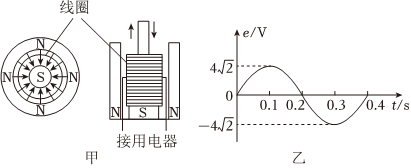
7.为发展新能源,某科研小组制作了一个小型波浪发电机,磁铁固定在水中,S极上套有一个浮筒,浮筒上绕有线圈,其截面示意图如图甲所示。浮筒可随波浪上下往复运动切割磁感线而产生电动势,线圈中产生的感应电动势随时间按正弦规律变化,如图乙所示,线圈电阻r=2Ω,把线圈与阻值R=8Ω的小灯泡串联,小灯泡恰好正常发光。下列说法正确的是( )
 组卷:116引用:4难度:0.5
组卷:116引用:4难度:0.5
四、论述、计算题(本题共4小题。共40分。解答应写出必要的文字说明、方程式和重要演算步骤,画出必要的示意图。有数值计算的题,答案中必须明确写出数值和单位)
-
22.传统航空母舰的阻拦系统原理如图甲所示,飞机着舰时,通过阻拦索对飞机施加作用力,使飞机在甲板上短距离滑行后停止。新一代航母阻拦系统的研制,则从阻拦索阻拦转向了引入电磁学模型的电磁阻拦技术,其基本原理如图乙所示,飞机着舰时钩住轨道上的一根金属棒并关闭动力系统,在磁场中共同滑行减速。
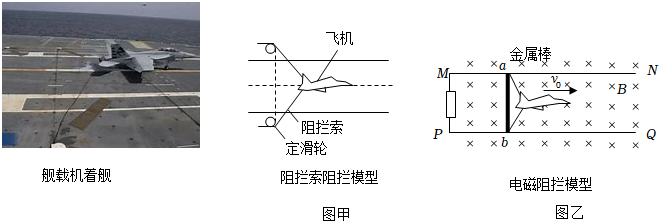
金属棒在导轨间宽为d,飞机质量为M,金属棒质量为m,飞机着舰钩住金属棒后与金属棒以共同速度v0进入磁场。轨道端点MP间电阻为R,金属棒电阻为r,不计其它电阻,且飞机阻拦索与金属棒绝缘。轨道间有竖直方向的匀强磁场,磁感应强度为B。金属棒运动L后飞机停下,测得此过程电阻R上产生焦耳热为Q,求:
(1)通过金属棒的最大电流;
(2)通过金属棒的电荷量;
(3)飞机和金属棒克服摩擦阻力和空气阻力所做的总功。组卷:581引用:5难度:0.5 -
23.2022年北京冬奥会自由式滑雪女子大跳台比赛中,中国队运动员谷爱凌力压世界排名第一的选手,最后一跳以向左偏轴转体1620°的动作完美逆转(如图1),获得个人首金。大跳台比赛比赛场地分为助滑区、起跳台、着陆坡和终点区域四个部分。图2是某技术公司对谷爱凌夺冠一跳的“高度-时间”分析。已知谷爱凌及身上的装置总质量为m=65kg。根据这些信息回答下述问题
(1)不考虑运动员转体的动作,将运动员看作质点。
a、设助滑出发区距地面高度为h1,运动员从静止出发,从起跳台起跳后能达到的最大高度距地面为h2,不计人体能量的消耗、不计一切摩擦,求运动员在最高点的速度大小v(用字母表示);
b、请你根据图2中的信息,估算v大小;
c、运动员落到着陆坡时,垂直坡面方向的速度在极短时间内减为0,因此运动员要承受极大的冲击力。设运动员在最高点速度约为v=20m/s,落到着陆坡时的速度方向与水平成α=45°,着陆坡的倾角θ=36°,雪板与坡面经大约Δt=0.05s的撞击时间后继续滑行。请根据以上条件估算运动员受到的冲击力。(保留1位有效数字)(可能会用到数据:sin36°=0.59,cos36°=0.81,sin9°=0.16,sin81°=0.99)(提示,先写表达式,再代数)。
(2)考虑运动员的转体动作。
a、若谷爱凌在空中腾空的时间约为3s,在空中转动的角速度几乎不变,求她在空中转动的角速度大小;
b、物体转动动能可以理解为各部分绕轴转动的动能之和。已知物体转动的惯性用物理量I来描述,它的名称为“转动惯量”,物体转动的快慢用角速度ω描述。请类比质点动能表达式,写出物体转动动能表达式;Ek=12mv2
c、若将谷爱凌在空中转动,理想化为一个半径约为0.20m的圆柱体的转动,已知圆柱体的转动惯量为(m为圆柱体质量,R为圆柱体半径),并假设谷爱凌在冲出跳台的瞬间(约0.02s)内获得足够的角速度,请问她瞬间转体爆发的功率大约多大?(保留1位有效数字)。I=12mR2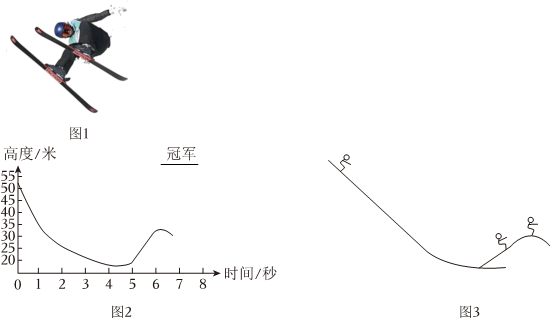 组卷:85引用:3难度:0.6
组卷:85引用:3难度:0.6


