2022-2023学年广东省汕头市龙湖区林百欣中学九年级（上）期中数学试卷

一、单选题（本大题10小题，每小题3分，共30分）

• 1．下列图形中，既是轴对称图形又是中心对称图形的是（　　）

  A．平行四边形

  B．正五边形

  C．圆

  D．等边三角形
  组卷：114引用：10难度：0.9

  解析

• 2．将二次函数y=x²的图象向右平移2个单位，再向上平移1个单位，所得图象的表达式是（　　）

  A．y=（x-2）2+1

  B．y=（x+2）2+1

  C．y=（x-2）2-1

  D．y=（x+2）2-1
  组卷：335引用：31难度：0.9

  解析

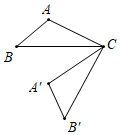• 3．如图，将△ABC就点C按逆时针方向旋转75°后得到△A′B′C，若∠ACB=25°，则∠BCA′的度数为（　　）

  A．50°

  B．40°

  C．25°

  D．60°
  组卷：971引用：14难度：0.8

  解析

• 4．已知函数y=（x-1）²+2，当函数值y随x的增大而减小时，x的取值范围是（　　）

  A．x＜1

  B．x＞1

  C．x＞-2

  D．-2＜x＜4
  组卷：159引用：4难度：0.6

  解析

• 5．根据下列表格的对应值：
  

  x	-1	1	1.1	1.2
  x2+12x-15	-26	-2	-0.59	0.84

  由此可判断方程x²+12x-15=0必有一个解x满足（　　）

  A．-1＜x＜1	B．1＜x＜1.1
  C．1.1＜x＜1.2	D．-0.59＜x＜0.84
  组卷：1534引用：17难度：0.7

  解析

• 6．如图，四边形ABCD是⊙O的内接四边形，BE是⊙O的直径，连接AE．若∠BCD=2∠BAD，则∠DAE的度数是（　　）

  A．30°

  B．35°

  C．45°

  D．60°
  组卷：2774引用：18难度：0.7

  解析

• 7．某经济开发区，今年一月份工业产值达50亿元，第一季度总产值为175亿元，二月、三月平均每月的增长率是多少若设平均每月的增长率为x,根据题意，可列方程为（　　）

  A．50（1+x）2=175

  B．50+50（1+x）+50（1+x）2=175

  C．50（1+x）+50（1+x）2=175

  D．50+50（1+x）2=175
  组卷：657引用：77难度：0.7

  解析

五、解答题（本大题2小题，每小题12分，共24分）

• 22．如图，△ABC和△DCE都是等边三角形．
  探究发现
  （1）△BCD与△ACE是否全等？若全等，加以证明；若不全等，请说明理由；
  拓展运用
  （2）若B、C、E三点不在一条直线上，∠ADC=30°，AD=3，CD=2，求BD的长；
  （3）若△DCE绕点C旋转，△ABC和△DCE的边长分别为1和2，当△BCD的面积最大时，AE的长为

  ．
  组卷：774引用：3难度：0.2

  解析

• 23．如图，已知直线y=

  4

  3

  x+4与x轴交于点A，与y轴交于点C，抛物线y=ax²+bx+c经过A，C两点，且与x轴的另一个交点为B，对称轴为直线x=-1．
  （1）求抛物线的表达式；
  （2）D是第二象限内抛物线上的动点，设点D的横坐标为m,求四边形ABCD面积S的最大值及此时D点的坐标；
  （3）若点P在抛物线对称轴上，是否存在点P，Q，使以点A，C，P，Q为顶点的四边形是以AC为对角线的菱形？若存在，请求出P，Q两点的坐标；若不存在，请说明理由．
  组卷：4185引用：18难度：0.1

  解析