2023年浙江省金华市六校中考数学第二次联谊试卷

一．选择题（本题有10小题，每小题3分，共30分）

• 1．-2022的相反数是（　　）

  A．- 1 2022

  B． 1 2022

  C．-2022

  D．2022
  组卷：1911引用：230难度：0.8

  解析

• 2．下列事件中，属于必然事件的是（　　）

  A．抛掷一枚均匀的硬币，恰好正面朝上

  B．打开数学书，恰好翻到第20页

  C．在1个标准大气压下，水加热到100℃沸腾

  D．打开电视机，它正在播新闻联播
  组卷：97引用：1难度：0.7

  解析

• 3．下列代数式变形中，是因式分解的是（　　）

  A． 1 2 ab（b-2）= 1 2 ab2-ab	B．3x-6y+3=3（x-2y）
  C．x2-3x+1=x（x-3）+1	D．-x2+2x-1=-（x-1）2
  组卷：420引用：7难度：0.7

  解析

• 4．若a＞b,则下列选项中，一定成立的是（　　）

  A．a+2＞b+2

  B．a-2＜b-2

  C．2a＜2b

  D．-2a＞-2b
  组卷：300引用：7难度：0.8

  解析

• 5．下面图形中是中心对称图形但不是轴对称图形的是（　　）
  

  A．科克曲线	B．笛卡尔心形线
  C．阿基米德螺旋线	D．赵爽弦图
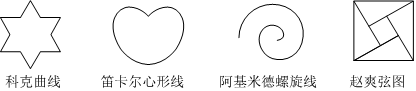  组卷：194引用：4难度：0.8

  解析

• 6．方差是刻画一组数据波动大小的量，对于一组数据x₁，x₂，x₃，…，x_n，可用如下算式计算方差：S²=

  1

  n

  [（x₁-3）²+（x₂-3）²+（x₃-3）²+…+（x_n-3）²]，其中“3”是这组数据的（　　）

  A．最小值

  B．平均数

  C．众数

  D．中位数
  组卷：536引用：10难度：0.9

  解析

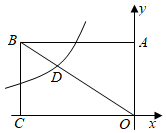• 7．如图，矩形OABC的面积为36，它的对角线OB与双曲线y=

  k

  x

  相交于点D，且OD：OB=2：3，则k的值为（　　）

  A．12

  B．-12

  C．16

  D．-16
  组卷：2540引用：15难度：0.6

  解析

• 8．已知线段AB，按如下步骤作图：
  ①取线段AB中点C；
  ②过点C作直线l,使l⊥AB；
  ③以点C为圆心，AB长为半径作弧，交l于点D；
  ④作∠DAC的平分线，交l于点E．则tan∠DAE的值为（　　）

  A． 1 2

  B． 2 5 5

  C． 5 + 1 2

  D． 5 - 1 2
  组卷：730引用：5难度：0.4

  解析

三．解答题（本题有8小题，共66分）

• 23．定义：若一个函数图象上存在横坐标是纵坐标两倍的点，则称该点为这个函数图象的“倍值点”，例如：点（2，1）是函数y=x-1的图象的“倍值点”．
  （1）分别判断函数y=

  1

  2

  x+1，y=x²-x的图象上是否存在“倍值点”？如果存在，求出“倍值点”的坐标；如果不存在，说明理由；
  （2）设函数y=

  2

  x

  （x＞0），y=-x+b的图象的“倍值点”分别为点A，B，过点B作BC⊥x轴，垂足为C．当△ABC的面积为2时，求b的值；
  （3）若函数y=x²-3（x≥m）的图象记为W₁，将其沿直线x=m翻折后的图象记为W₂，当W₁，W₂两部分组成的图象上恰有2个“倍值点”时，直接写出m的取值范围．
  组卷：358引用：1难度：0.6

  解析

• 24．在平面直角坐标系中，点B、E的坐标分别为B（-2，

  3

  ），E（4，0），过点E作直线l⊥x轴，设直线l上的动点A的坐标为（4，m），连接AB，将线段BA绕点B顺时针方向旋转30°得到线段BA′，在射线BA′上取点C，构造Rt△ABC，使得∠BAC=90°．
  （1）当m=-

  3

  时，求直线AB的函数表达式．
  （2）当点C落在坐标轴上时，求△ABC的面积．
  （3）已知点B关于原点O的对称点是点D，在点A的运动过程中，是否存在某一位置，使以A，C，D为顶点的三角形与△ABC相似？若存在，求出点A的坐标；若不存在，请说明理由．
  
  组卷：458引用：1难度：0.2

  解析