2023年广东省珠海市香洲区紫荆中学中考数学三模试卷

一.选择题（本大题10小题，每题3分，共30分）

• 1．在0，

  -

  1

  2

  ，-1，

  3

  这四个数中，最小的数是（　　）

  A．0

  B． - 1 2

  C．-1

  D． 3
  组卷：126引用：4难度：0.9

  解析

• 2．下列运算正确的是（　　）

  A．a2+2a2=3a4	B．（-a3）2=-a6
  C．（a+b）2=a2+b2	D．-2a8÷a2=-2a6
  组卷：142引用：2难度：0.7

  解析

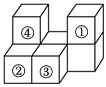• 3．如图，一个由7个小正方体组成的立体图形，拿走下列哪两个立体图形后，俯视图不会发生变化（　　）

  A．①和②

  B．②和③

  C．③和④

  D．①和④
  组卷：112引用：5难度：0.8

  解析

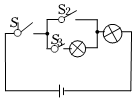• 4．如图，电路连接完好，且各元件工作正常．随机闭合开关S₁、S₂、S₃中的两个，能让两个小灯泡同时发光的概率为（　　）

  A． 1 6

  B． 1 2

  C． 2 3

  D． 1 3
  组卷：357引用：9难度：0.5

  解析

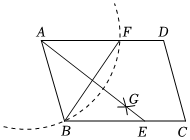• 5．如图，在平行四边形ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E，若BF=6，AB=5，则AE的长为（　　）

  A．10

  B．8

  C．6

  D．4
  组卷：407引用：17难度：0.6

  解析

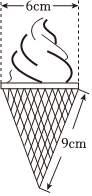• 6．如图，冰淇淋蛋筒下部呈圆锥形，则蛋筒圆锥部分包装纸的面积（接缝忽略不计）是（　　）

  A．27cm2

  B．54cm2

  C．27πcm2

  D．54πcm2
  组卷：1180引用：14难度：0.7

  解析

• 7．不等式组

  x + 1 ≥ 0

  x - 2 ＜ 1

  的解集在数轴上表示正确的是（　　）

  A．

  B．

  C．

  D．
  组卷：300引用：21难度：0.9

  解析

五.解答题（三）（本大题2小题，每题12分，共24分）

• 22．操作与研究：如图，△ABC被平行于CD的光线照射，CD⊥AB于D，AB在投影面上．
  （1）指出图中线段AC的投影是

  ，线段BC的投影是

  ．
  （2）问题情景：如图1，Rt△ABC中，∠ACB=90°，CD⊥AB，我们可以利用△ABC与△ACD相似证明AC²=AD×AB，这个结论我们称之为射影定理，请证明这个定理．
  （3）拓展运用如图2，正方形ABCD的边长为15，点O是对角线AC、BD的交点，点E在CD上，过点C作CF⊥BE，垂足为F，连接OF：
  ①试利用射影定理证明△BOF∽△BED；
  ②若DE=CE，求OF的长．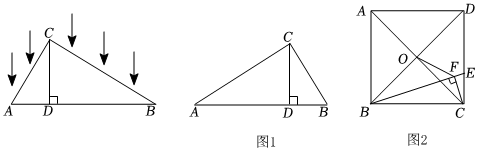
  
  组卷：207引用：1难度：0.2

  解析

• 23．如图，抛物线C₁：y=x²+bx+c与x轴交于A（-1，0），B（3，0）两点，与y轴交于点C．
  （1）直接写出抛物线C₁的解析式；
  （2）如图，有一宽度为1的直尺平行于y轴，直尺两长边被线段BC和抛物线C₁截得两线段DE、FG．设点D的横坐标为t,且0＜t＜2，当t为何值时四边形DEGF为平行四边形；
  （3）在（2）的条件下连接AF、CF，当直尺平行移动时，∠BAF与∠BCF能否相等？若能，求出t的值；若不能，请说明理由．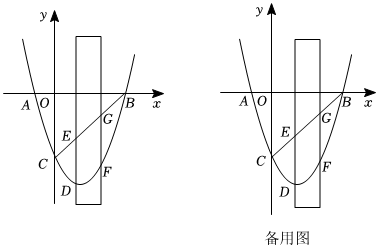
  
  组卷：117引用：1难度：0.2

  解析