2023-2024学年湖北省武汉市东西湖区九年级(上)期中数学试卷
发布:2024/10/2 6:0:2
一、选择题(本大题共10小题,每小题3分,共30分)
-
1.方程3x2=5x+7的二次项系数、一次项系数、常数项分别为( )
组卷:951引用:9难度:0.9 -
2.如图所示图案中,是中心对称图形的是( )
组卷:135引用:4难度:0.5 -
3.用配方法解方程x2+2x-5=0时,下列配方结果正确的是( )
组卷:141引用:6难度:0.9 -
4.下列方程中,没有实数根的是( )
组卷:41引用:1难度:0.5 -
5.把抛物线y=3x2向左平移2个单位,再向上平移1个单位,所得的抛物线的解析式是( )
组卷:1439引用:33难度:0.9 -
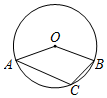 6.如图,A,B,C是⊙O上的三个点,如果∠AOB=140°,那么∠ACB的度数为( )组卷:430引用:6难度:0.6
6.如图,A,B,C是⊙O上的三个点,如果∠AOB=140°,那么∠ACB的度数为( )组卷:430引用:6难度:0.6 -
7.设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=x2-2x+c上的三点,y1,y2,y3的大小关系为( )
组卷:1855引用:17难度:0.5 -
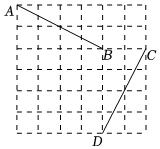 8.如图,在正方形网格中,点A的坐标为(0,5),点B的坐标为(4,3),线段AB绕着某点旋转一个角度与线段CD重合(C、D均为格点),若点A的对应点是点C,则它的旋转中心的坐标是( )组卷:503引用:7难度:0.6
8.如图,在正方形网格中,点A的坐标为(0,5),点B的坐标为(4,3),线段AB绕着某点旋转一个角度与线段CD重合(C、D均为格点),若点A的对应点是点C,则它的旋转中心的坐标是( )组卷:503引用:7难度:0.6
三、解答题(本题有8题,共72分)
-
23.如图,P是正方形ABCD内一点,将△ABP绕点B顺时针方向旋转 90° 得到△CBQ.
(1)观察猜想:如图1,线段AP与CQ的数量关系是 ,位置关系是 .
(2)探究实践:如图2,连接PC,若PA=1,PB=2,PC=3,求∠APB.
(3)拓展延伸:如图3,把BP绕点B在平面内自由旋转,若AB=BC=5,BP=2,当A,P,Q三点在一条直线上时,请直接写出AQ=.2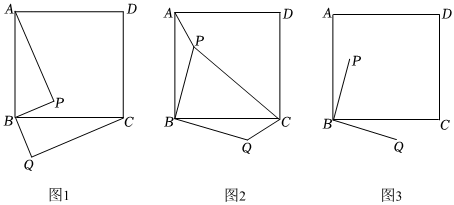 组卷:350引用:3难度:0.3
组卷:350引用:3难度:0.3 -
24.如图,直线l:y=-3x-3与x轴、y轴分别相交于A,B两点,与抛物线y=ax2+2ax+a-4交于点B.
(1)求该抛物线的解析式;
(2)已知点M是抛物线上的一个动点,并且点M在第三象限内,连接AM、BM,设点M的横坐标为m,四边形OAMB的面积为S,求S与m的函数表达式,并求出S的最大值;
(3)若点C在直线AB上,抛物线上是否存在点D使得以O,B,C,D为顶点的四边形是平行四边形.若存在,请直接写出点D的坐标.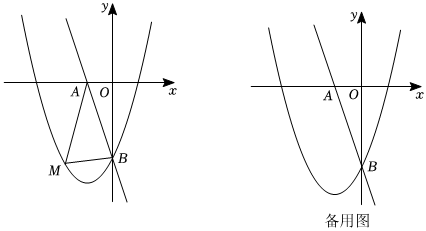 组卷:285引用:1难度:0.3
组卷:285引用:1难度:0.3


