2022-2023学年福建省厦门市海沧区北附学校八年级（上）期中数学试卷

一、选择题

• 1．下面四幅图分别是由体育运动长鼓舞、武术、举重、摔跤抽象出来的简笔画，其中是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：331引用：17难度：0.9

  解析

• 2．下列长度的三条线段首尾相连能组成三角形的是（　　）

  A．5，6，10

  B．2，5，8

  C．5，6，11

  D．3，4，8
  组卷：363引用：8难度：0.7

  解析

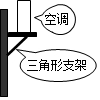• 3．如图，空调安装在墙上时，一般都会采用如图所示的方法固定，这种方法应用的几何原理是（　　）

  A．三角形两边之差小于第三边

  B．三角形两边之和大于第三边

  C．三角形的稳定性

  D．垂线段最短
  组卷：560引用：12难度：0.7

  解析

• 4．在实数0，-1，2，3中，最大的数是（　　）

  A．0

  B．-1

  C．2

  D．3
  组卷：8引用：2难度：0.5

  解析

• 5．已知图中的两个三角形全等，则∠α的度数是（　　）
  

  A．72°

  B．60°

  C．58°

  D．50°
  组卷：2267引用：47难度：0.7

  解析

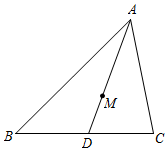• 6．如图，在△ABC中，AD交边BC于点D．设△ABC的重心为M，若点M在线段AD上，则下列结论正确的是（　　）

  A．∠BAD=∠CAD

  B．AM=DM

  C．△ABD的周长等于△ACD的周长

  D．△ABD的面积等于△ACD的面积
  组卷：662引用：6难度：0.7

  解析

• 7．为测量一池塘两端A，B间的距离．甲、乙两位同学分别设计了两种不同的方案．
  甲：如图1，先过点B作AB的垂线BF，再在射线BF上取C，D两点，使BC=CD，接着过点D作BD的垂线DE，交AC的延长线于点E．则测出DE的长即为A，B间的距离；
  乙：如图2，先确定直线AB，过点B作射线BE，在射线BE上找可直接到达点A的点D，连接DA，作DC=DA，交直线AB于点C，则测出BC的长即为AB间的距离，则下列判断正确的是（　　）

  A．只有甲同学的方案可行

  B．只有乙同学的方案可行

  C．甲、乙同学的方案均可行

  D．甲、乙同学的方案均不可行
  组卷：532引用：19难度：0.8

  解析

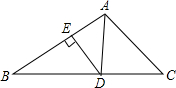• 8．如图，在△ABC中，AD平分∠BAC，DE⊥AB于E，S_△ABC=15，DE=3，AB=6，则AC长是（　　）

  A．7

  B．6

  C．5

  D．4
  组卷：2528引用：31难度：0.9

  解析

三、解答题

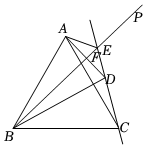• 24．如图，过等边△ABC的顶点B在△ABC内部作射线BP，设∠ABP=x（0°＜x＜30°），记点A关于射线BP的对称点为点D，直线CD交BP于点E，连接BD，AE．
  （1）求出∠CBD的大小；（用含x的式子表示）
  （2）试说明在∠ABP变化的过程中，∠BEC的大小保持不变，并求出∠BEC的大小；
  （3）连接AD，交BP于点F，用等式表示线段AE，BF，CE之间的数量关系，并予以证明．
  组卷：159引用：3难度：0.2

  解析

• 25．已知：如图1，平面直角坐标系中，点A的坐标是（0，6），点B在x轴上，且∠BAO=30°，点D是线段OA上的一点，以BD为边向下作等边△BDE．
  （1）如图2，当∠ODB=45°时，求证：OE平分∠BED．
  （2）如图3，当点E落在y轴上时，求出点E的坐标．
  （3）利用图1探究并说理：点D在y轴上从点A向点O滑动的过程中，点E也会在一条直线上滑动；并直接写出点E运动路径的长度．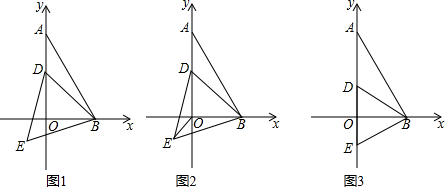
  
  组卷：754引用：10难度：0.3

  解析