2023-2024学年重庆市南岸区茶园新城中学九年级(上)月考数学试卷(10月份)
发布:2024/9/6 8:0:8
一、选择题(每小题4分,共40分)
-
1.小红有三顶帽子,分别为白色、红色和粉色,有两条围巾,分别为白色和红色.她随机拿出一顶帽子和一条围巾戴上,恰好为红色帽子和红色围巾的概率是( )
组卷:350引用:4难度:0.5 -
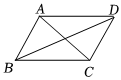 2.如图,要使平行四边形ABCD成为矩形,需要添加的条件是( )组卷:1450引用:11难度:0.9
2.如图,要使平行四边形ABCD成为矩形,需要添加的条件是( )组卷:1450引用:11难度:0.9 -
3.一元二次方程2x2-3x+1=0根的情况是( )
组卷:951引用:15难度:0.7 -
4.在一个不透明的盒子里装有若干个白球和15个红球,这些球除颜色不同外其余均相同,每次从袋子中摸出一个球记录下颜色后再放回,经过多次重复试验,发现摸到白球的频率稳定在0.4左右,则袋中白球约有( )
组卷:1406引用:21难度:0.9 -
5.一元二次方程x2-6x-5=0配方可变形为( )
组卷:625引用:16难度:0.7 -
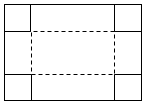 6.如图,把一块长为45cm,宽为25cm的矩形硬纸板的四角剪去四个相同的小正方形,然后把纸板沿虚线折起,做成一个无盖纸盒.若该无盖纸盒的底面积为625cm2,设剪去小正方形的边长为x cm,则可列方程为( )组卷:364引用:4难度:0.8
6.如图,把一块长为45cm,宽为25cm的矩形硬纸板的四角剪去四个相同的小正方形,然后把纸板沿虚线折起,做成一个无盖纸盒.若该无盖纸盒的底面积为625cm2,设剪去小正方形的边长为x cm,则可列方程为( )组卷:364引用:4难度:0.8 -
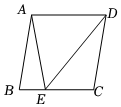 7.如图,已知E是菱形ABCD的边BC上一点,且∠DAE=∠B=80°,那么∠CDE的度数为( )组卷:948引用:4难度:0.6
7.如图,已知E是菱形ABCD的边BC上一点,且∠DAE=∠B=80°,那么∠CDE的度数为( )组卷:948引用:4难度:0.6 -
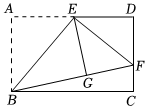 8.如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F,若AB=3,,则FD的长为( )BC=25组卷:232引用:3难度:0.6
8.如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F,若AB=3,,则FD的长为( )BC=25组卷:232引用:3难度:0.6
三、解答题(19题8分,其余各题每题10分,共78分)
-
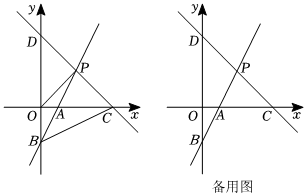 25.如图,在平面直角坐标系中,直线y=2x-2与x轴、y轴分别交于点A、点B,与直线CD:y=kx+b(k≠0)交于点P,OC=OD=4OA.
25.如图,在平面直角坐标系中,直线y=2x-2与x轴、y轴分别交于点A、点B,与直线CD:y=kx+b(k≠0)交于点P,OC=OD=4OA.
(1)求直线CD的解析式;
(2)连接OP、BC,若直线AB上存在一点Q,使得S△PQC=S四边形OBCP,求点Q的坐标;
(3)将直线CD向下平移1个单位长度得到直线,直线l与x轴交于点E,点N为直线l上的一点,在平面直角坐标系中,是否存在点M,使以点O,E,N,M为顶点的四边形是矩形?若存在,请直接写出点M的坐标;若不存在,请说明理由.组卷:1858引用:9难度:0.3 -
26.已知,在△ABC中,AC=BC,∠ACB=90°.
(1)如图1,点D、点E分别是线段AB上两点,连接CD、CE,若AD=BE,且∠ECD=45°,求∠ECB的度数;
(2)如图2,点D、点E分别是线段AB上两点,连接CD、CE,过点B作BF⊥AB交CE延长线于F,连接DF,若∠ECD=45°,求证:AD+BF=DF;
(3)如图3,M为射线AC上一点,N为射线CA上一点,且始终满足CM=AN,过点C作MB的垂线交AB的延长线于点P,连接NP,猜想:NP、MB、CP之间的数量关系并证明你的结论.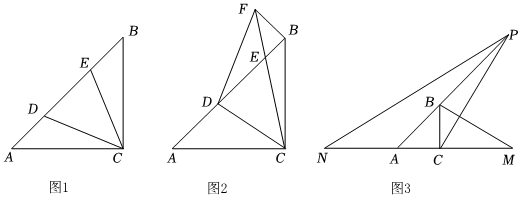 组卷:930引用:5难度:0.3
组卷:930引用:5难度:0.3


