2022-2023学年广东省深圳市南山区太子湾学校九年级（上）期中数学试卷

一．选择题（共10小题）

• 1．已知四条线段a,b,c,d是成比例线段，其中b=3cm,c=4cm,d=6cm,则线段a的长度为（　　）

  A．8cm

  B．2cm

  C．4cm

  D．1cm
  组卷：633引用：7难度：0.8

  解析

• 2．用3个同样的小正方体摆出的几何体，从三个方向看到的图形分别如图：
  
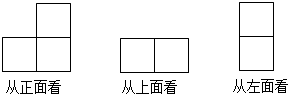
  这个几何体是（　　）

  A．

  B．

  C．

  D．
  组卷：1162引用：14难度：0.7

  解析

• 3．已知关于x的一元二次方程（k-2）x²-2x+1=0有两个不相等的实数根，则k的取值范围是（　　）

  A．k＜2

  B．k＜3

  C．k＜2且k≠0

  D．k＜3且k≠2
  组卷：1306引用：5难度：0.9

  解析

• 4．下列说法中错误的是（　　）

  A．直角三角形斜边上的中线等于斜边的一半

  B．菱形的对角线平分一组对角，并且菱形是轴对称图形

  C．矩形的对角线把这个矩形分成4个等腰三角形

  D．对角线互相垂直的菱形是正方形
  组卷：485引用：3难度：0.7

  解析

• 5．如图，一次函数y₁=k₁x+b与反比例函数y₂=

  k

  2

  x

  的图象相交于A，B两点，点A的横坐标为2，点B的横坐标为-1，则不等式k₁x+b＜

  k

  2

  x

  的解集是（　　）

  A．-1＜x＜0或x＞2	B．x＜-1或0＜x＜2
  C．x＜-1或x＞2	D．-1＜x＜2
  组卷：3699引用：16难度：0.7

  解析

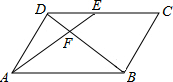• 6．如图，在平行四边形ABCD中，E为CD上一点，DE：CE=2：3．连接AE，BD交于点F，则S_△DEF：S_△ABF等于（　　）

  A．2：5

  B．2：25

  C．4：5

  D．4：25
  组卷：931引用：8难度：0.7

  解析

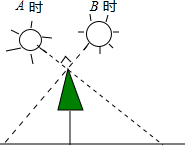• 7．如图，小明在A时测得某树的影长为3m,B时又测得该树的影长为2m,若两次日照的光线互相垂直，则树的高度为（　　）m.

  A． ± 6

  B． 6

  C．6

  D． 5
  组卷：892引用：5难度：0.5

  解析

三．解答题（共7小题）

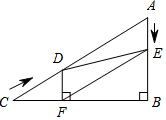• 21．如图，在Rt△ABC中，∠B=90°，AC=60cm,∠A=60°，点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D，E运动的时间是ts（0＜t≤15）．过点D作DF⊥BC于点F，连接DE，EF．
  （1）求证：四边形AEFD为平行四边形；
  （2）①当t=

  s时，四边形AEFD为菱形；
  ②当t=

  s时，四边形DEBF为矩形；
  组卷：1628引用：6难度：0.5

  解析

• 22．某数学活动小组在一次活动中，对一个数学问题做了如下研究：
  [问题发现]（1）如图①，在等边三角形ABC中，点M是BC上任意一点，连接AM，以AM为边作等边三角形AMN，连接CN，则∠ABC和∠ACN的数量关系为

  ．
  [变式探究]（2）如图②，在等腰三角形ABC中，AB=BC，点M是BC边上任意一点（不含端点B，C），连接AM，以AM为边作等腰三角形AMN，使∠AMN=∠ABC，AM=MN，连接CN，试探究∠ABC与∠ACN的数量关系，并说明理由；
  [解决问题]（3）如图③，在正方形ADBC中，点M为BC边上一点，以AM为边作正方形AMEF，点N为正方形AMEF的中心，连接CN，AB，AE，若正方形ADBC的边长为8，CN=

  2

  ，直接写出正方形AMEF的边长．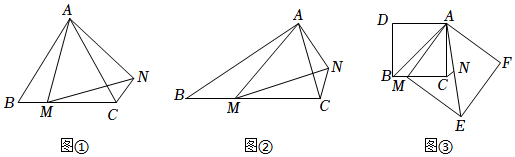
  
  组卷：736引用：5难度：0.2

  解析