2022-2023学年甘肃省陇南市礼县六中九年级（上）期中数学试卷

一、选择题。（本大题共10小题，每小题3分，共30分）

• 1．下列标志图中，既是轴对称图形，又是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：970引用：55难度：0.9

  解析

• 2．已知x=2是方程x²-px+2=0的一个实数根，那么p的值是（　　）

  A．-1

  B．-3

  C．1

  D．3
  组卷：194引用：8难度：0.7

  解析

• 3．将图绕其中心旋转某一角度后会与原图形重合，这个角不能是（　　）

  A．90°

  B．120°

  C．180°

  D．270°
  组卷：468引用：8难度：0.6

  解析

• 4．把抛物线y=x²+1向左平移1个单位，则平移后抛物线的解析式为（　　）

  A．y=（x+1）2+1

  B．y=（x-1）2+1

  C．y=x2+2

  D．y=x2
  组卷：607引用：7难度：0.6

  解析

• 5．抛物线y=-2x²+8x-8的对称轴是（　　）

  A．x=2

  B．x=-2

  C．x=4

  D．x=-4
  组卷：556引用：6难度：0.7

  解析

• 6．关于x的一元二次方程x²-4x+k-1=0两个相等的实数根，则关于x的一元二次方程x²-4x+k=0的根的情况是（　　）

  A．有两个不相等的实数根	B．有两个相等的实数根
  C．没有实数根	D．无法判定
  组卷：294引用：7难度：0.6

  解析

• 7．如图，在△ABC中，∠B=40°，将△ABC绕点A逆时针旋转，得到△ADE，点D恰好落在直线BC上，则旋转角的度数为（　　）

  A．70°

  B．80°

  C．90°

  D．100°
  组卷：363引用：22难度：0.7

  解析

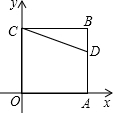• 8．如图，正方形OABC的两边OA、OC分别在x轴、y轴上，点D（5，3）在边AB上，以C为中心，把△CDB旋转90°，则旋转后点D的对应点D′的坐标是（　　）

  A．（-2，0）	B．（-2，10）
  C．（2，10）或（-2，0）	D．（10，2）或（-2，10）
  组卷：1076引用：10难度：0.7

  解析

• 9．如图，在长70m,宽40m的长方形花园中，欲修宽度相等的观赏路（如阴影部分所示），要使观赏路面积占总面积的

  1

  8

  ，则路宽x应满足的方程是（　　）

  A．（40-x）（70-x）=350	B．（40-2x）（70-3x）=2450
  C．（40-2x）（70-3x）=350	D．（40-x）（70-x）=2450
  组卷：753引用：31难度：0.7

  解析

四、解答题（二）。（本大题共5小题，共50分.解答时，应写出必要的文字说明、证明过程或演算步骤）

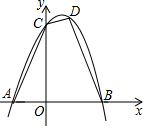• 27．如图，抛物线y=ax²+bx+6经过点A（-2，0），B（4，0），与y轴交于点C，点D是抛物线上的一个动点，设D的横坐标m（1＜m＜4），连接AC、BD、DC．
  （1）求该抛物线的函数解析式；
  （2）当CD∥AB时，求D点坐标；
  （3）连接BC，求△BCD面积的最大值及此时点D的坐标．
  组卷：437引用：4难度：0.5

  解析

• 28．如图，在正方形ABCD中，E、F分别是边CD、BC上的两点，且∠EAF=45°，AE、AF分别交正方形的对角线BD于G、H两点，将△ADE绕点A顺时针旋转90°后，得到△ABQ，连接EF．
  （1）求证：FA平分∠QAE．
  （2）求证：EF=BF+DE．
  （3）试试探索BH、HG、GD三条线段间的数量关系，并加以说明．
  组卷：486引用：8难度：0.4

  解析