当前位置：试卷中心 > 试卷详情

2023年陕西省中考数学试卷（A卷）

发布：2024/5/16 8:0:9

一、选择题（共8小题，每小题3分，计24分.每小题只有一个选项是符合题意的）

1．计算：3-5=（　　）
A．2 B．-2 C．8 D．-8
组卷：505引用：3难度：0.9
解析
2．下列图形中，既是轴对称图形，又是中心对称图形的是（　　）
A． B． C． D．
组卷：355引用：1难度：0.8
解析
3．如图，l∥AB，∠A=2∠B．若∠1=108°，则∠2的度数为（　　）
A．36° B．46° C．72° D．82°
组卷：1149引用：18难度：0.7
解析
4．计算：
6
x
y
2
•
（
-
1
2
x
3
y
3
）
=（　　）
A．3x⁴y⁵ B．-3x⁴y⁵ C．3x³y⁶ D．-3x³y⁶
组卷：1066引用：4难度：0.7
解析
5．在同一平面直角坐标系中，函数y=ax和y=x+a（a为常数，a＜0）的图象可能是（　　）
A． B．
C． D．
组卷：3395引用：21难度：0.7
解析
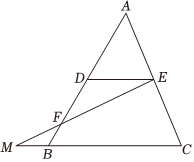6．如图，DE是△ABC的中位线，点F在DB上，DF=2BF．连接EF并延长，与CB的延长线相交于点M．若BC=6，则线段CM的长为（　　）
A．
13
2
B．7 C．
15
2
D．8
组卷：3586引用：30难度：0.5
解析
7．陕西饮食文化源远流长，“老碗面”是陕西地方特色美食之一．图②是从正面看到的一个“老碗”（图①）的形状示意图．
ˆ
AB
是⊙O的一部分，D是
ˆ
AB
的中点，连接OD，与弦AB交于点C，连接OA，OB．已知AB=24cm,碗深CD=8cm,则⊙O的半径OA为（　　）
A．13cm B．16cm C．17cm D．26cm
组卷：1961引用：19难度：0.7
解析
8．在平面直角坐标系中，二次函数y=x²+mx+m²-m（m为常数）的图象经过点（0，6），其对称轴在y轴左侧，则该二次函数有（　　）
A．最大值5 B．最大值
15
4
C．最小值5 D．最小值
15
4
组卷：3515引用：9难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（共13小题，计81分.解答应写出过程）

25．某校想将新建图书楼的正门设计为一个抛物线型拱门，并要求所设计的拱门的跨度与拱高之积为48m²，还要兼顾美观、大方，和谐、通畅等因素，设计部门按要求给出了两个设计方案．现把这两个方案中的拱门图形放入平面直角坐标系中，如图所示：
方案一，抛物线型拱门的跨度ON=12m,拱高PE=4m.其中，点N在x轴上，PE⊥ON，OE=EN．
方案二，抛物线型拱门的跨度ON′=8m,拱高P'E'=6m.其中，点N′在x轴上，P′E′⊥O′N′，OE′=E′N′．
要在拱门中设置高为3m的矩形框架，其面积越大越好（框架的粗细忽略不计）．方案一中，矩形框架ABCD的面积记为S₁，点A、D在抛物线上，边BC在ON上；方案二中，矩形框架A'B'C′D'的面积记为S₂，点A'，D'在抛物线上，边B'C'在ON'上．现知，小华已正确求出方案二中，当A'B'=3m时，
S
2
=
12
2
m
2
，请你根据以上提供的相关信息，解答下列问题：
（1）求方案一中抛物线的函数表达式；
（2）在方案一中，当AB=3m时，求矩形框架ABCD的面积S₁并比较S₁，S₂的大小．
组卷：2869引用：10难度：0.6
解析
26．（1）如图①，在△OAB中，OA=OB，∠AOB=120°，AB=24．若⊙O的半径为4，点P在⊙O上，点M在AB上，连接PM，求线段PM的最小值；
（2）如图②所示，五边形ABCDE是某市工业新区的外环路，新区管委会在点B处，点E处是该市的一个交通枢纽．已知：∠A=∠ABC=∠AED=90°，AB=AE=10000m,BC=DE=6000m.根据新区的自然环境及实际需求，现要在矩形AFDE区域内（含边界）修一个半径为30m的圆型环道⊙O；过圆心O，作OM⊥AB，垂足为M，与⊙O交于点N．连接BN，点P在⊙O上，连接EP．其中，线段BN、EP及MN是要修的三条道路，要在所修道路BN、EP之和最短的情况下，使所修道路MN最短，试求此时环道⊙O的圆心O到AB的距离OM的长．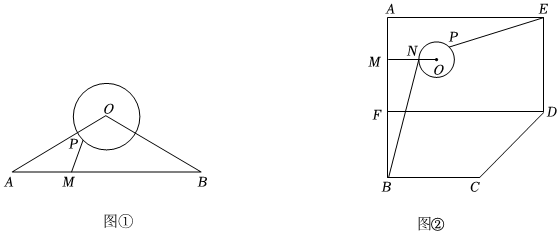
组卷：1733引用：1难度：0.5
解析