2023-2024学年福建省泉州市晋江一中、华侨中学九年级(上)月考数学试卷(9月份)
发布:2024/9/20 16:0:8
一.选择题(本大题共10小题,共40分.在每小题列出的选项中,选出符合题目的一项)
-
1.若式子
在实数范围内有意义,则x的取值范围是( )x-2组卷:219引用:5难度:0.9 -
2.下列二次根式是最简二次根式的是( )
组卷:686引用:9难度:0.8 -
3.用配方法解一元二次方程x2-8x+2=0,此方程可化为的正确形式是( )
组卷:1881引用:25难度:0.4 -
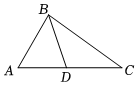 4.下列条件不能判定△ADB∽△ABC的是( )组卷:2290引用:25难度:0.7
4.下列条件不能判定△ADB∽△ABC的是( )组卷:2290引用:25难度:0.7 -
5.杭州亚运会吉祥物深受大家喜爱.某商户3月份销售吉祥物“宸宸”摆件为10万个,5月份销售11.5万个.设该摆件销售量的月平均增长率为x(x>0),则可列方程为( )
组卷:1334引用:18难度:0.8 -
 6.如图,已知AB∥CD∥EF,BC:CE=3:4,AF=21,那么DF的长为( )组卷:2000引用:18难度:0.7
6.如图,已知AB∥CD∥EF,BC:CE=3:4,AF=21,那么DF的长为( )组卷:2000引用:18难度:0.7 -
7.下列说法正确的是( )
组卷:1233引用:6难度:0.5 -
8.已知等腰三角形的两边长分别是一元二次方程x2-7x+10=0的两根,则该等腰三角形的周长为( )
组卷:1094引用:12难度:0.6
三.解答题(本大题共9小题,共86分.解答应写出文字说明,证明过程或演算步骤)
-
24.关于x的方程:2(x-k)=x-4①和关于x的一元二次方程:(k-1)x2+2mx+(3-k)+n=0②(k、m、n均为实数),方程①的解为非正数.
(1)求k的取值范围;
(2)如果方程②的解为负整数,k-m=2,2k-n=6且k为整数,求整数m的值;
(3)当方程②有两个实数根x1、x2,满足(x1+x2)(x1-x2)+2m(x1-x2+m)=n+5,且k为正整数,试判断|m|≤2是否成立?请说明理由.组卷:606引用:5难度:0.4 -
25.[初步尝试]
(1)如图①,在三角形纸片ABC中,∠ACB=90°,将△ABC折叠,使点B与点C重合,折痕为MN,则AM与BM的数量关系为 ;
[思考说理]
(2)如图②,在三角形纸片ABC中,AC=BC=6,AB=10,将△ABC折叠,使点B与点C重合,折痕为MN,求的值;AMBM
[拓展延伸]
(3)如图③,在三角形纸片ABC中,AB=9,BC=6,∠ACB=2∠A,将△ABC沿过顶点C的直线折叠,使点B落在边AC上的点B′处,折痕为CM.
①求线段AC的长;
②若点O是边AC的中点,点P为线段OB′上的一个动点,将△APM沿PM折叠得到△A′PM,点A的对应点为点A′,A′M与CP交于点F,求的取值范围.PFMF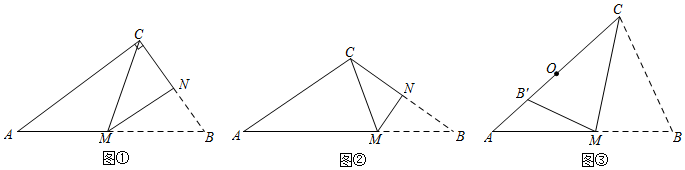 组卷:5197引用:17难度:0.1
组卷:5197引用:17难度:0.1


