2023-2024学年浙江省职教高考研究联合体高三(上)第一次调研数学试卷(9月份)
发布:2024/10/22 0:0:2
一、单项选择题(本大题共20小题,1-10小题每小题2分,11-20小题每小题2分,共50分)
-
1.已知集合A={-3,-1,0,1}B={-2,-1,1,2},则A∩B等于( )
组卷:45引用:1难度:0.9 -
2.在实数范围内,“x=-2”是“x3=-8”的( )
组卷:52引用:1难度:0.9 -
3.已知A(-2,3),B(1,2)两点,则
等于( )BA组卷:53引用:1难度:0.7 -
4.已知角α=2024°,则角α的终边所在的象限是( )
组卷:78引用:1难度:0.8 -
5.已知A(2,3),B(4,1)两点,且点C是线段AB的中点,则点C的坐标为( )
组卷:29引用:1难度:0.8 -
6.已知
,且角α为第四象限角,则sinα等于( )cosα=15组卷:62引用:1难度:0.7 -
7.不等式|3-2x|>1的解集为( )
组卷:75引用:2难度:0.8 -
8.函数
的定义域为( )f(x)=log2x+x-1+1x+1组卷:32引用:1难度:0.8 -
9.现有5名学生站成一排照相,其中甲同学必须站在最中间的站法有( )
组卷:30引用:1难度:0.8 -
10.若二次函数f(x)=x2+kx+4的最小值为3,则常数k等于( )
组卷:35引用:2难度:0.8 -
11.如图所示,椭圆的标准方程为( )
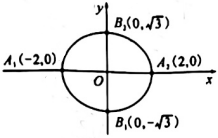 组卷:50引用:1难度:0.9
组卷:50引用:1难度:0.9
三、解答题(本大题共8小题,共72分)
-
34.已知等差数列{an}满足a2+a8=14,a3-a7=-4,等比数列{bn}满足b1+a1=4,b2+a2=6.
(1)求数列{an},{bn}的通项公式;
(2)设cn=,求数列{cn}的前n项和Sn.2(an-2)log2bn+2组卷:38引用:1难度:0.5 -
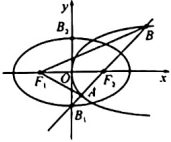 35.如图所示,已知椭圆C1=1(a>b>0)的离心率:x2a2+y2b2,短轴长|B1B2|=2抛物线C2的顶点在坐标原点,对称轴为x轴,焦点与椭圆C1的右焦后F2重合.e=22
35.如图所示,已知椭圆C1=1(a>b>0)的离心率:x2a2+y2b2,短轴长|B1B2|=2抛物线C2的顶点在坐标原点,对称轴为x轴,焦点与椭圆C1的右焦后F2重合.e=22
(1)求椭圆C1与抛物线C2的标准方程;
(2)若直线l经过点F1,且倾斜角α满足,且直线l与抛物线C2相交于A,B两点,求△ABF1的面积.cosα=22组卷:10引用:1难度:0.5


