2022-2023学年广东省惠州市惠阳区金辉学校八年级（上）月考数学试卷（9月份）

一、选择题（共10题，共30分）

• 1．已知△ABC≌△A′B′C′，∠A=40°，∠C=110°，则∠B'的度数是（　　）

  A．30°

  B．40°

  C．50°

  D．110°
  组卷：17引用：2难度：0.7

  解析

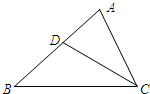• 2．如图，在△ABC中，CD是∠ACB的平分线，∠A=80°，∠ACB=60°，那么∠BDC=（　　）

  A．80°

  B．90°

  C．100°

  D．110°
  组卷：458引用：37难度：0.9

  解析

• 3．已知△ABC内一点P，如果点P到AB、AC两边的距离相等，则点P（　　）

  A．在BC边的垂直平分线上

  B．在BC边的高上

  C．在BC边所对角的平分线上

  D．在BC边的中线上
  组卷：714引用：7难度：0.9

  解析

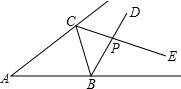• 4．如图，△ABC的外角的平分线BD与CE相交于点P，若点P到AC的距离为3，则点P到AB的距离为（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：2663引用：20难度：0.6

  解析

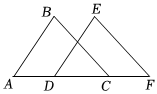• 5．如图，已知点A、D、C、F在同一直线上，AB=DE，AD=CF，添加下列条件后，仍不能判断△ABC≌△DEF的是（　　）

  A．BC=EF

  B．∠A=∠EDF

  C．AB∥DE

  D．∠BCA=∠EDF
  组卷：960引用：6难度：0.7

  解析

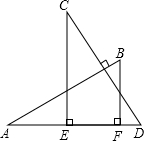• 6．如图，AB⊥CD，CE⊥AF，BF⊥ED．若AB=CD，CE=8，BF=6，AD=10，则EF的长为（　　）

  A．4

  B． 7 2

  C．3

  D． 5 2
  组卷：469引用：3难度：0.7

  解析

• 7．一个多边形的内角和等于它的外角和的3倍，它是（　　）

  A．八边形

  B．七边形

  C．六边形

  D．五边形
  组卷：409引用：7难度：0.9

  解析

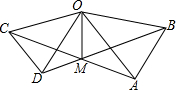• 8．如图，在△OAB和△OCD中，OA=OB，OC=OD，OA＞OC，∠AOB=∠COD=40°，连接AC，BD交于点M，连接OM．下列结论：①AC=BD；②∠AMB=40°；③OM平分∠BOC；④MO平分∠BMC．其中正确的个数为（　　）

  A．4

  B．3

  C．2

  D．1
  组卷：13677引用：83难度：0.5

  解析

三、解答题（共8题，共62分）

• 24．【问题情境】
  如图1：在△ABC中，AB=AC，点P为边BC上的任意一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D、E，过点B作BG⊥AC，垂足为G．
  求证：PD+PE=BG．
  【变化一下】
  当点P在BC延长线上时，请画图探究PD、PE、BG三者之间的数量关系并给出证明：
  （2）如图2，△ABC满足AB=AC=BC，点P为△ABC内任意一点，过点P分别作PD⊥AB，PE⊥AC，PF⊥BC，垂足分别为D、E、F，请直接写出PD、PE、PF和BG之间的关系．
  【深入探究】
  如图3，在△ABC中，点P为△ABC内任意一点，过点P分别作PD⊥AB，PE⊥AC，PF⊥BC，垂足分别为D、E、F，过点A、B、C分别作AI⊥BC，BG⊥AC，CH⊥AB，垂足分别为I、G、H，记CH、BG、AI分别为h₁、h₂、h₃，请直接写出PD、PE、PF和h₁、h₂、h₃之间的关系．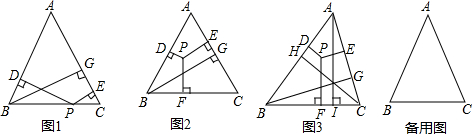
  组卷：804引用：5难度：0.1

  解析

• 25．（1）如图1，已知：在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m,CE⊥直线m,垂足分别为点D、E．证明：DE=BD+CE．
  （2）如图2，将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．
  （3）拓展与应用：如图3，D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA=∠AEC=∠BAC，试判断△DEF的形状．
  
  组卷：11394引用：145难度：0.5

  解析