2023年山东省日照市东港区曲阜师大附属学校中考数学三模试卷

一、选择题

• 1．-

  1

  2

  的相反数是（　　）

  A． 1 2

  B．2

  C．-2

  D．- 1 2
  组卷：3011引用：744难度：0.9

  解析

• 2．下列图案中，既是轴对称图形又是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：38引用：3难度：0.9

  解析

• 3．计算：a²-（a+1）（a-1）的结果是（　　）

  A．1

  B．-1

  C．2a2+1

  D．2a2-1
  组卷：847引用：34难度：0.9

  解析

• 4．如图，数轴的原点未标注，数轴的单位长度为1，数轴上的点B和点C表示的数的绝对值相等，那么可以判断点A表示的数是（　　）

  A．-2

  B．-3

  C．-4

  D．-6
  组卷：131引用：4难度：0.7

  解析

• 5．我们知道三角形的内角和为180°，而四边形可以分成两个三角形，故它的内角和为2×180°=360°，五边形则可以分成3个三角形，它的内角和为3×180°=540°（如图），依此类推，则八边形的内角和为（　　）
  

  A．900°

  B．1080°

  C．1260°

  D．1440°
  组卷：268引用：4难度：0.5

  解析

• 6．为做好疫情防控工作，在学校门口放置了A，B，C三条体温检测通道，某日入校张老师与王同学走相同通道的概率为（　　）

  A． 1 2

  B． 1 3

  C． 1 4

  D． 1 5
  组卷：48引用：4难度：0.7

  解析

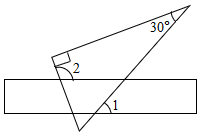• 7．将含30°角的一个直角三角板和一把直尺如图放置，若∠1=50°，则∠2等于（　　）

  A．80°

  B．100°

  C．110°

  D．120°
  组卷：882引用：16难度：0.7

  解析

三、解答题

• 21．【问题解决】
  一节数学课上，老师提出了这样一个问题：如图1，点P是正方形ABCD内一点，PA=1，PB=2，PC=3．你能求出∠APB的度数吗？
  小明通过观察、分析、思考，形成了如下思路：
  思路一：将△BPC绕点B逆时针旋转90°，得到△BP′A，连接PP′，求出∠APB的度数；
  思路二：将△APB绕点B顺时针旋转90°，得到△CP'B，连接PP′，求出∠APB的度数．
  请参考小明的思路，任选一种写出完整的解答过程．
  【类比探究】
  如图2，若点P是正方形ABCD外一点，PA=3，PB=1，PC=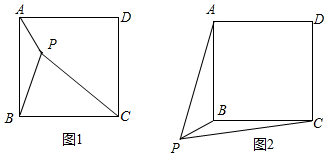

  11

  ，求∠APB的度数．
  
  组卷：4566引用：16难度：0.1

  解析

• 22．如图，已知直线y=

  4

  3

  x+4与x轴交于点A，与y轴交于点C，抛物线y=ax²+bx+c经过A，C两点，且与x轴的另一个交点为B，对称轴为直线x=-1．
  （1）求抛物线的表达式；
  （2）D是第二象限内抛物线上的动点，设点D的横坐标为m,求四边形ABCD面积S的最大值及此时D点的坐标；
  （3）若点P在抛物线对称轴上，是否存在点P，Q，使以点A，C，P，Q为顶点的四边形是以AC为对角线的菱形？若存在，请求出P，Q两点的坐标；若不存在，请说明理由．
  组卷：4152引用：18难度：0.1

  解析