2023年贵州省铜仁市沿河县第一教育集团中考数学一模试卷

一、选择题（本大题共12小题，每题3分，共36分）

• 1．下列四个数中，最小的数是（　　）

  A．0

  B．-2

  C．1

  D． 2
  组卷：274引用：10难度：0.9

  解析

• 2．如图所示的几何体是由4个完全相同的小正方体搭成的，它的主视图是（　　）

  A．

  B．

  C．

  D．
  组卷：341引用：3难度：0.9

  解析

• 3．位于我县境内的沙沱水电站，属“西电东送”第二批开工项目的“4水工程”之一．年平均发电量45.89亿kW．h.数“45.89亿”用科学记数法表示为（　　）

  A．4.589×108

  B．4.589×109

  C．4.589×1010

  D．4.589×1011
  组卷：74引用：1难度：0.9

  解析

• 4．如图，直线c与直线a、b都相交．若a∥b,∠1=55°，则∠2=（　　）

  A．125°

  B．55°

  C．115°

  D．45°
  组卷：48引用：1难度：0.7

  解析

• 5．在函数y=

  9

  -

  3

  x

  中，自变量x的取值范围是（　　）

  A．x≤3

  B．x＜3

  C．x≥3

  D．x＞3
  组卷：1207引用：6难度：0.8

  解析

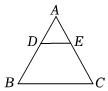• 6．如图，在△ABC中，DE∥BC，DE=2，BC=5，则S_△ADE：S_△ABC的值是（　　）

  A． 3 25

  B． 4 25

  C． 2 5

  D． 3 5
  组卷：2732引用：13难度：0.7

  解析

• 7．两个不透明的口袋中各有三个相同的小球，将每个口袋中的小球分别标号为1，2，3．从这两个口袋中分别摸出一个小球，则下列事件为随机事件的是（　　）

  A．两个小球的标号之和等于1

  B．两个小球的标号之和等于6

  C．两个小球的标号之和大于1

  D．两个小球的标号之和大于6
  组卷：987引用：21难度：0.9

  解析

• 8．我国魏晋时期的数学家赵爽在为天文学著作《周髀算经》作注解时，用4个全等的直角三角形和中间的小正方形拼成一个大正方形，这个图被称为“弦图”，它体现了中国古代数学的成就．如图，已知大正方形ABCD的面积是100，小正方形EFGH的面积是4，那么tan∠ADF（　　）

  A． 4 3

  B． 3 4

  C． 4 5

  D． 3 5
  组卷：127引用：1难度：0.5

  解析

三、解答题（本大题共7个题，共102分）

• 24．小红看到一处喷水景观，喷出的水柱呈抛物线形状，她对此展开研究：测得喷水头P距地面0.7m,水柱在距喷水头P水平距离5m处达到最高，最高点距地面3.2m；建立如图所示的平面直角坐标系，并设抛物线的表达式为y=a（x-h）²+k,其中x（m）是水柱距喷水头的水平距离，y（m）是水柱距地面的高度．
  （1）求抛物线的表达式．
  （2）爸爸站在水柱正下方，且距喷水头P水平距离3m.身高1.6m的小红在水柱下方走动，当她的头顶恰好接触到水柱时，求她与爸爸的水平距离．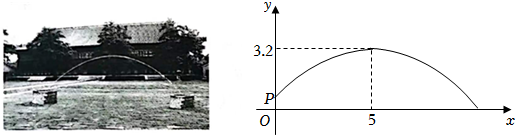
  
  组卷：4966引用：40难度：0.6

  解析

• 25．同学们还记得吗？图①是我们研究过的湘教版八年级上册教材P99第16题“已知，如图在等腰三角形ABC中，∠C=90°，D是AB的中点，DE⊥DF点E、F分别在AC、AB上求证：DE=DF”的图形；图②是我们研究过的湘教版九年级上册教材P90第2题“如图，AB⊥BD，ED⊥BD，C是BD的中点．已知ED=1，BD=4，求AB的长．”的图形，受这两个图形的启发，数学兴趣小组提出了以下三个问题，请你回答：
  
  （1）【问题一】受图①启发，兴趣小组画出了图③，正方形ABCD的对角线相交于点O，点O又是正方形A₁B₁C₁O的一个顶点，OA₁交AB于点E，OC₁交BC于点F，则AE与BF的数量关系为

  ；
  （2）【问题二】受图①启发，兴趣小组画出了图④：直线m、n经过正方形ABCD的对称中心O，直线m分别与AD、BC交于点E、F，直线n分别与AB、CD交于点G、H，且m⊥n,若正方形ABCD边长为8，求四边形OEAG的面积；
  （3）【问题三】受图②启发，兴趣小组画出了图⑤：正方形CEFG的顶点G在正方形ABCD的边CD上，顶点E在BC的延长线上，且BC=6，CE=2．在直线BE上是否存在点P，使△APF为直角三角形？若存在，求出BP的长度；若不存在，说明理由．
  组卷：380引用：1难度：0.1

  解析