2022-2023学年甘肃省庆阳市九年级（上）期中数学试卷

一、选择题：本大题共10个小题，每小题3分，共30分．每小题只有一个正确选项

• 1．下列平面图形中，既是轴对称图形又是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：21引用：4难度：0.9

  解析

• 2．在平面直角坐标系中，点（3，-2）关于原点对称点的坐标是（　　）

  A．（3，2）

  B．（-3，-2）

  C．（-3，2）

  D．（3，-2）
  组卷：382引用：30难度：0.9

  解析

• 3．用配方法解一元二次方程x²-4x-5=0时，下列变形正确的是（　　）

  A．（x+2）2=1

  B．（x-2）2=5

  C．（x-2）2=9

  D．（x-2）2=21
  组卷：61引用：6难度：0.7

  解析

• 4．一元二次方程2x²+2x+3=0的根的情况是（　　）

  A．有两个相等的实数根	B．有两个不相等的实数根
  C．只有一个实数根	D．无实数根
  组卷：120引用：3难度：0.5

  解析

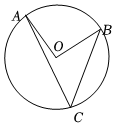• 5．已知：如图，OA，OB是⊙O的两条半径，且OA⊥OB，点C在⊙O上，则∠ACB的度数为（　　）

  A．45°

  B．35°

  C．25°

  D．20°
  组卷：20引用：3难度：0.8

  解析

• 6．关于二次函数y=2（x-3）²+1，下列说法正确的是（　　）

  A．图象的开口向下

  B．图象的对称轴为直线x=-3

  C．图象顶点坐标为（3，-1）

  D．当x＜3时，y随x的增大而减小
  组卷：1188引用：9难度：0.5

  解析

• 7．某超市一月份的营业额为36万元，三月份的营业额为48万元，设每月的平均增长率为x,则可列方程为（　　）

  A．48（1-x）2=36	B．48（1+x）2=36
  C．36（1-x）2=48	D．36（1+x）2=48
  组卷：1372引用：137难度：0.9

  解析

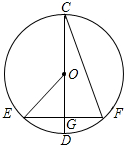• 8．如图，⊙O的直径CD过弦EF的中点G，∠DCF=20°，则∠EOD等于（　　）

  A．10°

  B．20°

  C．40°

  D．80°
  组卷：76引用：69难度：0.9

  解析

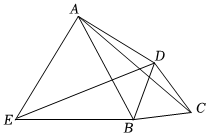• 9．如图，在四边形ABCD中，∠DAB=30°，连接AC，将△ABC绕点B按逆时针方向旋转60°得到△EBD，点C的对应点与点D重合，若AB=5，AD=4，则AC的长度为（　　）

  A．6

  B． 6 2

  C．7

  D． 41
  组卷：12引用：2难度：0.5

  解析

四、解答题（二）：本大题共5小题，共40分．解答应写出必要的文字说明，证明过程或演算步骤．

• 27．【模型】如图1，已知△BAD和△BCE均为等腰直角三角形，∠BAD=∠BCE=90°，点M为DE的中点．过点E与AD平行的直线交射线AM于点N，则点M为AN的中点．
  
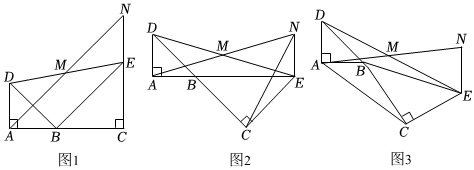
  【拓展】
  （1）如图2，将图1中△BCE绕点B旋转，当A，B，E三点在同一直线上时，求证：△CAN为等腰直角三角形．
  【迁移】
  （2）如图3，将图1中△BCE绕点B旋转，当A，B，E三点不在同一直线上时，（2）中的结论是否仍然成立？若成立，请证明；若不成立，请说明理由．
  组卷：35引用：2难度：0.2

  解析

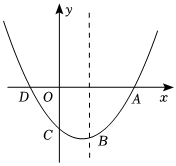• 28．如图，已知抛物线y=

  3

  8

  x²-

  3

  4

  x-3与x轴的交点为A、D（A在D的右侧），与y轴的交点为C．
  （1）直接写出A、D、C三点的坐标；
  （2）若点M在抛物线对称轴上，使得MD+MC的值最小，并求出点M的坐标；
  （3）设点C关于抛物线对称轴的对称点为B，在抛物线上是否存在点P，使得以A、B、C、P四点为顶点的四边形为梯形？若存在，请求出点P的坐标；若不存在，请说明理由．
  组卷：2713引用：54难度：0.1

  解析