2023-2024学年北京市丰台十二中八年级（上）月考数学试卷（10月份）
发布：2024/9/2 4:0:8
一、选择题（每题3分，共30分）
-
1．如图，用三角板作△ABC的边AB上的高线，下列三角板的摆放位置正确的是（ ）
组卷：307引用：7难度：0.8 -
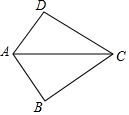2．如图，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（ ）组卷：4577引用：128难度：0.7 -
3．如图，AD是∠CAE的平分线，∠B=35°，∠DAE=60°，那么∠ACB等于（ ）组卷：121引用：4难度：0.9 -
4．如果一个多边形的内角和是外角和的3倍，则这个多边形的边数是（ ）
组卷：4560引用：71难度：0.9 -
5．满足下列条件的△ABC中，不是直角三角形的是（ ）
组卷：528引用：17难度：0.7 -
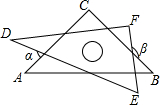6．小明把一副含45°，30°的直角三角板如图摆放，其中∠C=∠F=90°，∠A=45°，∠D=30°，则∠α+∠β等于（ ）组卷：8490引用：64难度：0.7 -
7．AD是△ABC中BC边上的中线，若AB=4，AC=6，则AD的取值范围是（ ）
组卷：222引用：1难度：0.5 -
8．如图，在△ABC中，∠C=90°，AC=BC，AD是∠CAB的角平分线，DE⊥AB于点E，若AB=6cm,则△DEB的周长是（ ）组卷：602引用：17难度：0.9 -
9．如图，在△ABC中，P为BC上一点，PR⊥AB，垂足为R，PS⊥AC，垂足为S，∠CAP=∠APQ，PR=PS，下面的结论：①AS=AR；②QP∥AR；③△BRP≌△CSP．其中正确的是（ ）组卷：827引用：11难度：0.5
三、解答题（23、24题每题5分；25至28题每题6分，共34分）
-
27．问题背景：如图①，已知△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m,CE⊥直线m,垂足分别为点D，E，易证：DE=+．
拓展延伸：如图②，将（1）中的条件改为：在△ABC中，AB=AC，D，A，E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC，请求出DE，BD，CE三条线段的数量关系，并证明．
实际应用：如图③，在△ACB中，∠ACB=90°，AC=BC，点C的坐标为（-2，0），点A的坐标为（-6，3），请直接写出B点的坐标．
组卷：439引用：7难度：0.3 -
28．如图，Rt△ACB中，∠ACB=90°，AC=BC，E点为射线CB上一动点，连接AE，作AF⊥AE且AF=AE．
（1）如图1，过F点作FD⊥AC交AC于D点，求证：FD=BC；
（2）如图2，连接BF交AC于G点，若AG=3，CG=1，求证：E点为BC中点；
（3）当E点在射线CB上，连接BF与直线AC交于G点，若BC=4，BE=3，则=（直接写出结果）AGCG
组卷：846引用：10难度：0.3
