2022-2023学年上海市宝山区高二(下)期末数学试卷
发布:2024/5/11 8:0:9
一、填空题(本大题共有12题,满分54分,其中1-6题每题4分,7-12题每题5分)【考生应在答题纸相应编号的空格内直接填写结果.】
-
1.直线x=1的倾斜角为
.组卷:190引用:6难度:0.7 -
2.在空间直角坐标系O-xyz中,点P(1,2,4)关于xOy平面的对称点Q的坐标为 .
组卷:38引用:4难度:0.9 -
3.直线l过点(2,3),且与向量
垂直,则直线l的方程为 .a=(1,2)组卷:68引用:3难度:0.8 -
4.双曲线
的两条渐近线的夹角的余弦值为 .x24-y2=1组卷:41引用:2难度:0.7 -
5.某产品经过4次革新后,成本由原来的200元下降到125元.如果这种产品每次革新后成本下降的百分比相同,那么每次革新后成本下降的百分比是 (结果精确到0.1%).
组卷:40引用:2难度:0.8 -
6.若2x2+(m2+m)y2+2mx+m=0表示圆,则实数m的值为 .
组卷:269引用:3难度:0.7 -
7.已知实数a,b,c成等差数列,则直线ax+by+c=0必过定点 .
组卷:109引用:7难度:0.8
三、解答题(本大题共有5题,满分78分)【解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.】
-
20.在数列{an}中,
.在等差数列{bn}中,前n项和为Sn,b1=2,2b3+S5=28.an=-1n=12an-1+3n≥2
(1)求数列{an}和{bn}的通项公式;
(2)设数列{cn}满足cn=(an+3bn)cosnπ,数列{cn}的前n项和记为Tn,试判断是否存在正整数m,使得Tm=2023?若存在,求出m的值;若不存在,说明理由.组卷:82引用:3难度:0.5 -
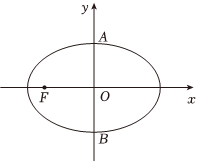 21.已知椭圆Γ:的焦距为2,且过点x2a2+y2b2=1(a>b>0).(1,22)
21.已知椭圆Γ:的焦距为2,且过点x2a2+y2b2=1(a>b>0).(1,22)
(1)求椭圆Γ的标准方程;
(2)A、B分别为椭圆Γ的上、下顶点,O为坐标原点,过椭圆Γ的左焦点F作直线l交椭圆Γ于C、D两点,与y轴交于M点.
①若点Q是线段CD的中点,求点Q的轨迹方程;
②设直线AD与直线BC交于点N,求证:为定值.OM•ON组卷:74引用:2难度:0.5


