当前位置：试卷中心 > 试卷详情

2022-2023学年陕西省西安市莲湖区庆安中学七年级（下）月考数学试卷（3月份）

发布：2024/8/18 5:0:1

一、单选题（每题3分）

1．计算（-x）³•（-x）²的结果是（　　）
A．x⁵ B．-x⁵ C．x⁶ D．-x⁶
组卷：167引用：4难度：0.9
解析
2．已知a=81³¹，b=27⁴¹，c=9⁶¹，则a,b,c的大小关系是（　　）
A．a＞b＞c B．a＞c＞b C．c＞b＞a D．b＞c＞a
组卷：2380引用：14难度：0.7
解析
3．已知a^m=2，aⁿ=3，则a^3m+2n的值是（　　）
A．6 B．24 C．36 D．72
组卷：2797引用：17难度：0.9
解析
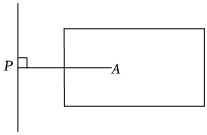4．如图，是测量学生跳远成绩的示意图，即PA的长为某同学的跳远成绩，其依据是（　　）
A．两点之间线段最短
B．两点确定一条直线
C．垂线段最短
D．过一点有且只有一条直线与已知直线垂直
组卷：208引用：9难度：0.8
解析
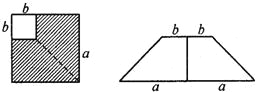
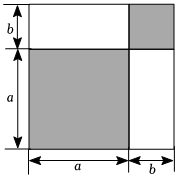
5．如图，在边长为a的正方形上剪去一个边长为b的小正方形（a＞b），把剩下的部分剪拼成一个梯形，分别计算这两个图形阴影部分的面积，由此可以验证的等式是（　　）
A．a²-b²=（a+b）（a-b） B．（a+b）²=a²+2ab+b²
C．（a-b）²=a²-2ab+b² D．a²-ab=a（a-b）
组卷：1734引用：65难度：0.9
解析
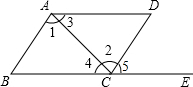6．如图，点E在BC延长线上，下列条件中，不能推断AB∥CD的是（　　）
A．∠4=∠3 B．∠1=∠2
C．∠B=∠5 D．∠B+∠BCD=180°
组卷：1145引用：28难度：0.9
解析
7．计算（a-b）（a+b）（a²+b²）（a⁴-b⁴）的结果是（　　）
A．a⁸+2a⁴b⁴+b⁸ B．a⁸-2a⁴b⁴+b⁸
C．a⁸+b⁸ D．a⁸-b⁸
组卷：8899引用：55难度：0.7
解析
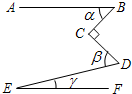8．如图，AB∥EF，∠C=90°，则α、β和γ的关系是（　　）
A．β=α+γ B．α+β+γ=180° C．α+β-γ=90° D．β+γ-α=180°
组卷：3204引用：20难度：0.9
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题

23．通常，用两种不同的方法计算同一个图形的面积可以得到一个恒等式图将一个边长为a+b的正方形图形分割成四部分（两个正方形和两个长方形），请观察图形，解答下列问题：
（1）根据图中条件，用两种方法表示该图形的总面积，可得如下公式：
；
（2）如果图中的a、b（a＞b＞0）满足a²+b²=70，ab=15，求a+b的值；
（3）已知（x+9）²+（x-1）²=124，求（x+9）（x-1）．
组卷：586引用：9难度：0.6
解析
24．配方法是数学中重要的一种思想方法．它是指将一个式子的某一部分通过恒等变形化为完全平方式或几个完全平方式的和的方法．这种方法常被用到代数式的变形中，并结合非负数的意义来解决一些问题．我们定义：一个整数能表示成a²+b²（a、b是整数）的形式，则称这个数为“完美数”．例如，5是“完美数”．理由：因为5=2²+1²，所以5是“完美数”．
解决问题：
（1）已知29是“完美数”，请将它写成a²+b²（a、b是整数）的形式
；
（2）若x²-6x+5可配方成（x-m）²+n（m、n为常数），则mn=
；
探究问题：
（1）已知x²+y²-2x+4y+5=0，则x+y=
；
（2）已知S=x²+4y²+4x-12y+k（x、y是整数，k是常数），要使S为“完美数”，试求出符合条件的一个k值，并说明理由．
拓展结论：
已知实数x、y满足
-
x
2
+
5
2
x
+
y
-
5
=
0
，求x-2y的最值．
组卷：951引用：12难度：0.7
解析