2023年山东省泰安六中新校中考数学二模试卷

一、选择题（本大题共12小题，满分36分）

• 1．下列互为倒数的是（　　）

  A．3和 1 3

  B．-2和2

  C．3和 - 1 3

  D．-2和 1 2
  组卷：1209引用：26难度：0.9

  解析

• 2．下列计算中正确的是（　　）

  A．a3•a3=a9	B．（-2a）3=-8a3
  C．a10÷（-a2）3=a4	D．（-a+2）（-a-2）=a2+4
  组卷：691引用：13难度：0.7

  解析

• 3．在一些美术字中，有的汉字是轴对称图形．下面4个汉字中，可以看作是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：623引用：20难度：0.9

  解析

• 4．如图，直线l₁∥l₂，AB=AC，∠BAC=40°，则∠1+∠2的度数是（　　）

  A．60°

  B．70°

  C．80°

  D．90°
  组卷：1270引用：7难度：0.7

  解析

• 5．为有效防控新冠疫情，国家大力倡导全国人民免费接种疫苗．截止至2022年5月底，我国疫苗接种高达339000万剂次．数据339000万用科学记数法可表示为a×10⁹的形式，则a的值是（　　）

  A．0.339

  B．3.39

  C．33.9

  D．339
  组卷：339引用：8难度：0.7

  解析

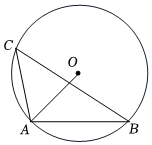• 6．如图，△ABC内接于⊙O，∠C=46°，连接OA，则∠OAB=（　　）

  A．44°

  B．45°

  C．54°

  D．67°
  组卷：2411引用：19难度：0.6

  解析

• 7．今年我国小麦大丰收，农业专家在某种植片区随机抽取了10株小麦，测得其麦穗长（单位：cm）分别为8，8，6，7，9，9，7，8，10，8，那么这一组数据的方差为（　　）

  A．1.5

  B．1.4

  C．1.3

  D．1.2
  组卷：692引用：3难度：0.7

  解析

• 8．如图，在▱ABCD中，AD=2，AB=4，∠A=30°，以点A为圆心，AD的长为半径画弧交AB于点E，连接CE，则阴影部分的面积是（　　）

  A． 3 - π 3

  B． 3 - π 6

  C． 4 - π 3

  D． 4 - π 6
  组卷：1429引用：9难度：0.7

  解析

三、解答题（共7小题）​

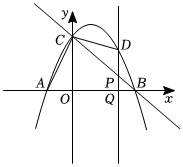• 24．如图所示，在平面直角坐标系中，直线y=-x+3交坐标轴于B、C两点，抛物线y=ax²+bx+3经过B、C两点，且交x轴于另一点A（-1，0）．点D为抛物线在第一象限内的一点，过点D作DQ∥CO，DQ交BC于点P，交x轴于点Q．
  （1）求抛物线的解析式；
  （2）设点P的横坐标为m,在点D的移动过程中，存在∠DCP=∠DPC，求出m值；
  （3）在抛物线上取点E，在平面直角坐标系内取点F，问是否存在以C、B、E、F为顶点且以CB为边的矩形？如果存在，请求出点F的坐标；如果不存在，请说明理由．
  组卷：751引用：7难度：0.2

  解析

• 25．问题背景：某学习小组正在研究如下问题：如图1所示，四边形ABCD与四边形CEFG均为正方形，且点E、G分别在边BC、CD上，连接DE、BG，点M是BG中点，连接CM，试猜测CM与DE的数量关系与位置关系，并加以证明．
  解决问题：小华从旋转的角度提出一个问题：如图2，将正方形CEFG绕点C顺时针旋转一定角度，其他条件不变，此时“问题背景”中的结论还成立吗？如果成立，请加以证明；如果不成立，请说明理由．
  拓展延伸：小刚提出了一个更加一般化的问题：如图3所示，▱ABCD∽▱ECGF，且

  AB

  BC

  =

  a

  b

  ，其他条件不变，此时CM与DE又有怎样的数量关系？请直接写出结果．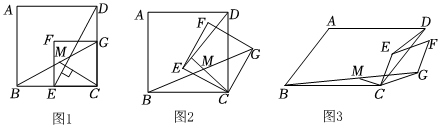
  ​
  组卷：245引用：4难度：0.1

  解析