2023-2024学年北京市西城区回民中学九年级（上）期中数学试卷

一、选择题（本题共16分，每小题2分）下面各题均有四个选项，其中只有一个是符合题意的

• 1．生活中有许多对称美的图形，下列是中心对称图形但不是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：1011引用：24难度：0.9

  解析

• 2．抛物线y=-（x+1）²-2的对称轴是（　　）

  A．x=1

  B．x=-1

  C．x=2

  D．x=-2
  组卷：610引用：6难度：0.8

  解析

• 3．一元二次方程x²-8x-1=0配方后可变形为（　　）

  A．（x+4）2=17

  B．（x-4）2=17

  C．（x+4）2=15

  D．（x-4）2=15
  组卷：1345引用：251难度：0.7

  解析

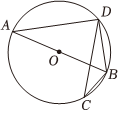• 4．如图，若AB是⊙O的直径，CD是⊙O的弦，∠ABD=58°，则∠BCD的度数为（　　）

  A．32°

  B．58°

  C．64°

  D．116°
  组卷：304引用：7难度：0.7

  解析

• 5．底面半径为3，高为4的圆锥侧面积为（　　）

  A．15π

  B．20π

  C．25π

  D．30π
  组卷：433引用：6难度：0.6

  解析

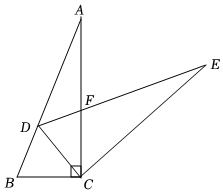• 6．如图．△ABC中，∠ACB=90°，将△ABC绕点C顺时针旋转得到△EDC，使点B的对应点D恰好落在AB边上，AC、ED交于点F．若∠BCD=α，则∠EFC的度数是（用含α的代数式表示）（　　）

  A．90°+ 1 2 α

  B．90°- 1 2 α

  C．180°- 3 2 α

  D． 3 2 α
  组卷：2907引用：21难度：0.5

  解析

• 7．已知抛物线y=ax²+bx+c（a＞0）的对称轴为直线x=-1，与x轴的一个交点为（x₁，0），且0＜x₁＜1，下列结论：①9a-3b+c＞0；②b-2a=0；③3a+c＜0；④a-b＜an²+bn（n≠-1的实数）．其中正确结论的个数是（　　）

  A．0

  B．1

  C．2

  D．3
  组卷：76引用：1难度：0.5

  解析

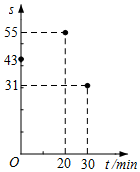• 8．心理学家发现：课堂上，学生对概念的接受能力s与提出概念的时间t（单位：min）之间近似满足函数关系s=at²+bt+c（a≠0），s值越大，表示接受能力越强．如图记录了学生学习某概念时t与s的三组数据，根据上述函数模型和数据，可推断出当学生接受能力最强时，提出概念的时间为（　　）

  A．8min

  B．13min

  C．20min

  D．25min
  组卷：700引用：9难度：0.6

  解析

二、填空题（本题共16分，每小题2分）.

• 9．已知x=1是关于x的方程x²+mx+n=0的一个根，则m+n的值是

  ．
  组卷：578引用：15难度：0.8

  解析

三、解答题（本题共68分，第18-23题，每小题6分，第17、24、25、26题，每小题6分，第27、28题，每小题6分）

• 27．如图，在△ABC中，∠ACB=90°，AC=BC，P，D为射线AB上两点（点D在点P的左侧），且PD=BC，连接CP．以P为中心，将线段PD逆时针旋转n°（0＜n＜180）得线段PE．
  
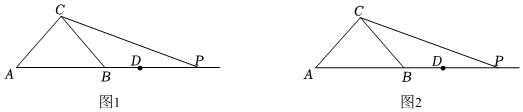
  （1）如图1，当四边形ACPE是平行四边形时，画出图形，并直接写出n的值；
  （2）当n=135°时，M为线段AE的中点，连接PM．
  ①在图2中依题意补全图形；
  ②用等式表示线段CP与PM之间的数量关系，并证明．
  组卷：755引用：5难度：0.2

  解析

• 28．对于平面直角坐标系xOy中的图形M和点P，给出如下定义：将图形M绕点P顺时针旋转90°得到图形N，图形N称为图形M关于点P的“垂直图形”．例如，图1中点D为点C关于点P的“垂直图形”
  （1）点A关于原点O的“垂直图形”为点B．
  ①若点A的坐标为（0，2），则点B的坐标为

  ；
  ②若点B的坐标为（2，1），则点A的坐标为

  ；
  （2）E（-3，3），F（-2，3），G（a,0）．线段EF关于点G的“垂直图形”记为E′F′，点E的对应点为E′，点F的对应点为F′．
  ①求点E′的坐标（用含a的式子表示）；
  ②若⊙O的半径为2，E′F′上任意一点都在⊙O内部或圆上，直接写出满足条件的EE′的长度的最大值．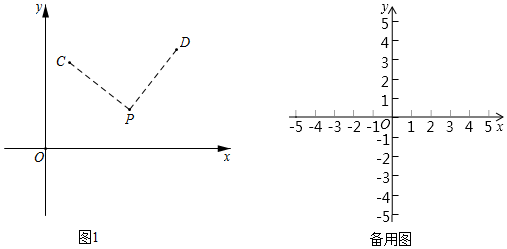
  
  组卷：860引用：5难度：0.1

  解析