2021-2022学年山西省太原市小店区志达中学九年级（上）月考数学试卷（12月份）

一、选择题（本大题共10个小题，在每个小题给出的四个选项中，只有一项符合题目要求，请选出并在答题卡上将该选项涂黑）

• 1．泰勒斯是古希腊时期的思想家，科学家，哲学家，他最早提出了命题的证明．泰勒斯曾通过测量同一时刻标杆的影长，标杆的高度，金字塔的影长，推算出金字塔的高度，这种测量原理，就是我们所学的（　　）

  A．图形的平移	B．图形的旋转
  C．图形的轴对称	D．图形的相似
  组卷：1254引用：37难度：0.7

  解析

• 2．如图，过反比例函数y=

  k

  x

  （x＞0）的图象上一点A作AB⊥x轴于点B，连接AO，若S_△AOB=2，则k的值为（　　）

  A．2

  B．3

  C．4

  D．5
  组卷：7703引用：53难度：0.9

  解析

• 3．下列各图形中一定是相似图形的是（　　）

  A．两个菱形	B．两个正方形
  C．两个直角三角形	D．两个矩形
  组卷：62引用：3难度：0.6

  解析

• 4．对于反比例函数y=

  4

  x

  ，下列说法不正确的是（　　）

  A．这个函数的图象分布在第一、三象限

  B．这个函数的图象既是轴对称图形又是中心对称图形

  C．点（1，4）在这个函数图象上

  D．当x＞0时，y随x的增大而增大
  组卷：1033引用：6难度：0.7

  解析

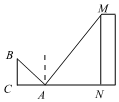• 5．如图，小明为了测量高楼MN的高度，在离点N18米的点A处放了一个平面镜，小明沿NA方向后退1.5米到点C，此时从镜子中恰好看到楼顶的点M，已知小明的眼睛（点B）到地面的高度BC是1.6米，则高楼MN的高度是（　　）

  A．18.5米

  B．18.8米

  C．19.2米

  D．21.3米
  组卷：375引用：5难度：0.6

  解析

• 6．若点A（-1，y₁），B（2，y₂），C（3，y₃）在反比例函数y=-

  6

  x

  的图象上，则y₁，y₂，y₃的大小关系是（　　）

  A．y1＞y2＞y3

  B．y2＞y3＞y1

  C．y1＞y3＞y2

  D．y3＞y2＞y1
  组卷：3706引用：80难度：0.6

  解析

• 7．如图，点D是△ABC的边AB上的一点，连接DC，则下列条件中不能判定△ABC∽△ACD的是（　　）

  A．∠B=∠ACD

  B．∠ADC=∠ACB

  C． AC CD = AB BC

  D． AC AD = AB AC
  组卷：562引用：8难度：0.7

  解析

三、解答题（本大题共5个小题，解答应写出文字说明，证明过程或演算步骤）

• 20．综合与实践
  课程学习：矩形折纸中的数学．
  动手操作
  如图1，四边形ABCD是一张矩形纸片，先将矩形ABCD沿AD，BC边的点E，F对折，使得AB与CD重合，折痕为EF，把这个矩形展平．
  （1）数学思考
  求证：四边形ABFE是矩形：
  （2）继续操作：
  如图2，陈老师在图1的基础上，沿直线BG折叠，使A点落在EF上，对应点为H，再沿直线DM折叠，使C点落在EF上，对应点为N：
  解决问题：
  试判断线段BH与DN的位置关系并证明
  （3）受到陈老师的启发，小卫和小韩在图2的基础上分别提出了不同的问题，请你帮助她们解决提出的问题；
  ①小卫：若图2中的点N、H恰好是线段EF的三等分点，延长线段DN，交BC于点Q，得到如图3所示的图形，试说明点Q是BF的中点；
  ②小韩：若图2中矩形的边AB的长为4，AD的长为6，请直接写出线段FM的长度．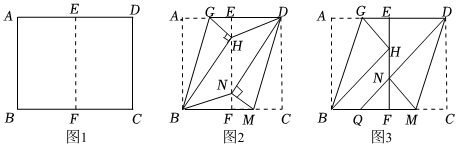
  
  组卷：56引用：2难度：0.3

  解析

• 21．综合与探究．
  如图，抛物线y=x²+2x-8与x轴交于A，B两点（点A在点B左侧），与y轴交于点C．
  （1）求A，B，C三点的坐标．
  （2）连接AC，直线x=-m（-4≤m＜0）与抛物线交于点E，与AC交于点D，m为何值时线段DE的长度最大，最大值是多少？
  （3）在（2）中线段DE取得最大值的条件下，若点N是直线DE上一点，点M是抛物线上一点，是否存在点M，N使得以A，C，M，N为顶点的四边形是平行四边形？若存在，请直接写出点M的坐标；若不存在，请说明理由．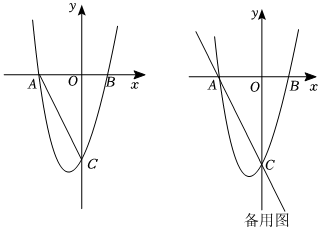
  
  组卷：38引用：1难度：0.4

  解析