2023-2024学年山西省大同六中九年级（上）第一次月考数学试卷

一.选择题（每小题3分，共30分）

• 1．如图，下列所给图形中是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：22引用：1难度：0.8

  解析

• 2．下列一元二次方程没有实数根的是（　　）

  A．x2+2x+1=0

  B．x2+x+2=0

  C．x2-1=0

  D．x2-2x-1=0
  组卷：4307引用：49难度：0.7

  解析

• 3．将抛物线y=2（x+1）²-3平移后与抛物线y=2x²重合，那么平移的方法可以是（　　）

  A．向右平移1个单位，再向上平移3个单位

  B．向右平移1个单位，再向下平移3个单位

  C．向左平移1个单位，再向上平移3个单位

  D．向左平移1个单位，再向下平移3个单位
  组卷：370引用：5难度：0.6

  解析

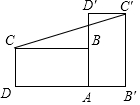• 4．如图，把矩形ABCD绕点A顺时针旋转，使点B的对应点B落在DA的延长线上，若AB=2，BC=4，则点C与其对应点C的距离为（　　）

  A．6

  B．8

  C．2 5

  D．2 10
  组卷：399引用：6难度：0.8

  解析

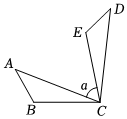• 5．如图，将△ABC绕点C顺时针旋转80°，得到△DEC，若∠B=3∠A=120°，则∠a的度数是（　　）

  A．60°

  B．50°

  C．40°

  D．30°
  组卷：86引用：1难度：0.6

  解析

• 6．对于二次函数y=-（x-2）²-7，下列说法正确的是（　　）

  A．图象开口向上

  B．对称轴是直线x=-2

  C．当x＞2时，y随x的增大而减小

  D．当x＜2时，y随x的增大而减小
  组卷：74引用：1难度：0.5

  解析

• 7．用配方法解方程x²+8x+7=0，变形后的结果正确的是（　　）

  A．（x+4）2=-7

  B．（x+4）2=9

  C．（x+4）2=23

  D．（x+4）2=-9
  组卷：359引用：8难度：0.6

  解析

三、解答题（共75分）

• 22．如图①，在正方形ABCD中，点E为DC边上一点，连接AE，点F为AE的中点，过点E作EG⊥AC于点G．连接DF，FG．
  观察猜想：
  （1）①∠DFG与∠DAC的数量关系是

  ；
  ②DF和FG的数量关系是

  ．
  探究发现：
  （2）将图1中△EGC绕点C逆时针旋转，使点E恰好落在AC上，将线段DF绕点F旋转180°得到线段HF，连接DG，HG，HE，如图2所示，探究DG和HG的数量关系，并说明理由．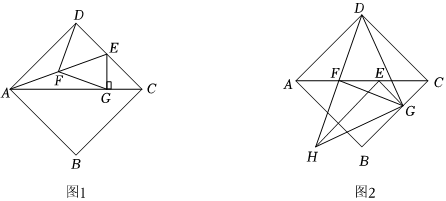
  组卷：35引用：1难度：0.5

  解析

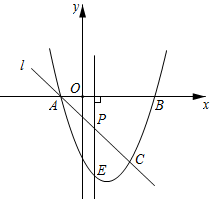• 23．如图，抛物线y=x²+bx+c与x轴交于A（-1，0），B（3，0）两点，过点A的直线l交抛物线于点C（2，m）．
  （1）求抛物线的解析式．
  （2）点P是线段AC上一个动点，过点P作x轴的垂线交抛物线于点E，求线段PE最大时点P的坐标．
  （3）点F是抛物线上的动点，在x轴上是否存在点D，使得以点A，C，D，F为顶点的四边形是平行四边形？如果存在，请直接写出所有满足条件的点D的坐标；如果不存在，请说明理由．
  组卷：4738引用：21难度：0.1

  解析