2023年山西省百校联考中考数学模拟试卷（二）

一、选择题（本大题共10个小题，每小题3分，共30分．在每个小题的四个选项中，只有一项符合题目要求，请选出并在答题卡上将该项涂黑）

• 1．下列各数中，最小的数是（　　）

  A．1

  B． 1 2

  C．0

  D．-1
  组卷：105引用：54难度：0.9

  解析

• 2．2022年第22届国际足联世界杯在卡塔尔举办．下列四届世界杯会徽中是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：147引用：6难度：0.9

  解析

• 3．下列调查中，最适合采用普查方式的是（　　）

  A．市场监督管理局对当地粮食加工品质量安全的调查

  B．2023年中央电视台春节联欢晚会收视率的调查

  C．九年级某班学生每周参加体育锻炼时长的调查

  D．全市初中学生参加家务劳动情况的调查
  组卷：91引用：3难度：0.8

  解析

• 4．下列运算正确的是（　　）

  A． 3 - 2 = 1

  B． 1 . 6 = 0 . 4

  C． （ 2 2 ） 2 = 4 2

  D． 27 - 3 = 2 3
  组卷：54引用：2难度：0.6

  解析

• 5．水盂是文房第五宝，古时用于给砚池添水，如图是清晚时期六方水盂，则它的主视图是（　　）

  A．

  B．

  C．

  D．
  组卷：136引用：4难度：0.8

  解析

• 6．如图，将△ABC沿BC方向平移得到△A'B'C'．连接AA'，若AA'=3cm,BC'=11cm,则B'C的长为（　　）

  A．3cm

  B．4cm

  C．5cm

  D．6cm
  组卷：373引用：11难度：0.6

  解析

• 7．已知反比例函数

  y

  =

  k

  x

  （

  k

  ≠

  0

  ）

  的图象经过点（2，3），则下列描述正确的是（　　）

  A．y的值随x值的增大而减小

  B．图象位于第二、四象限

  C．当x＞0时，y＜0

  D．点（3，2）在图象上
  组卷：201引用：1难度：0.7

  解析

三、解答题（本大题共8个小题，共75分．解答应写成必要的文字说明，演算步骤或推理过程）

• 22．综合与实践
  问题情境：四边形ABCD是菱形，∠ABC=60°，点P是菱形边上或内部一点，连接AP，BP，∠APB=60°，点E在线段BP上，点F在线段AP上，且BE=AF，连接AE，EF，

  AB

  =

  2

  7

  ，∠AEF=30°．
  （1）特例感知：如图1，当点P与点C重合时，△EFC的形状是

  ，AE²+EF²=

  ．
  （2）深入探究：如图2，当点P在菱形内部时，连接CE，CF，判断（1）中的两个结论是否仍然成立，并说明理由．
  （3）拓展应用：如图3，在（2）的条件下，连接CP，若EF⊥AP，直接写出四边形ECPF的面积．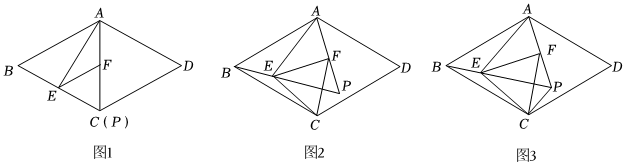
  
  组卷：336引用：1难度：0.4

  解析

• 23．综合与探究
  如图1，抛物线y=ax²+bx+3（a≠0）与x轴交于A（-2，0），B（4，0）两点，与y轴交于点C，点P是抛物线在第二象限内的一个动点，过点P作PD∥y轴交直线BC于点D，连接PC，PB．设点P的横坐标为m.
  （1）求抛物线的函数表达式．
  （2）①请用含m的代数式表示△PBC的面积．
  ②当△PBC的面积为

  15

  4

  时，求点P的坐标．
  （3）如图2，在（2）②的条件下，点Q是射线CO上的一个动点，射线PQ交直线BC于点G，当△CQG是等腰三角形时，请直接写出所有满足条件的点Q的坐标．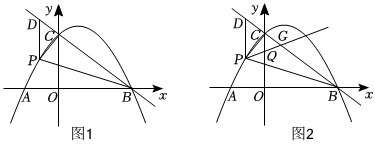
  
  组卷：242引用：1难度：0.1

  解析