当前位置：试卷中心 > 试卷详情

2022-2023学年湖南省长沙一中双语实验学校九年级（上）第三次月考数学试卷

发布：2024/8/19 3:0:0

一、单选题（共30分）

1．下列各式中，结果是2022的是（　　）
A．-（+2022） B．-（-2022） C．-|-2022| D．-|+2022|
组卷：20引用：3难度：0.8
解析
2．多项式3x²-8yx²-3xy³+1是（　　）
A．三次四项式 B．三次三项式 C．四次四项式 D．四次三项式
组卷：30引用：1难度：0.7
解析
3．如图，四个几何体分别为四棱锥、三棱柱、圆柱体和长方体，这四个几何体中截面可能是圆形的几何体是（　　）
A．
四棱锥 B．
三棱柱 C．
圆柱体 D．
长方体
组卷：172引用：3难度：0.7
解析
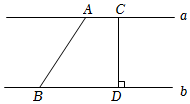4．如图，直线a∥b,则直线a,b之间的距离是（　　）
A．线段AB B．线段AB的长度
C．线段CD D．线段CD的长度
组卷：360引用：4难度：0.7
解析
5．下列是方程2x+y=7的解的是（　　）
A．
x
=
-
1
y
=
5
B．
x
=
1
y
=
5
C．
x
=
3
y
=
4
D．
x
=
4
y
=
3
组卷：600引用：4难度：0.7
解析
6．下列说法正确的是（　　）
A．a不是负数，则a＞0 B．m不小于-1，则m＞-1
C．a+b是负数，则a+b＜0 D．b是不大于0的数，则b＜0
组卷：136引用：5难度：0.8
解析
7．下列长度的三条线段，首尾相连能组成三角形的是（　　）
A．2cm、2cm、4cm B．2cm、4cm、6cm
C．4cm、10cm、4cm D．3cm、4cm、5cm
组卷：57引用：3难度：0.8
解析

8．下列命题错误的是（　　）

A．三角形的三条高交于一点

B．三角形的三条中线都在三角形内部

C．直角三角形的三条高交于一点，且交点在直角顶点处

D．三角形的三条角平分线交于一点，且这个交点到三角形三边的距离相等

组卷：103引用：3难度：0.6

解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（共72分）

24．定义：若两个函数的图象关于某一点Q中心对称，则称这两个函数关于点Q互为“对称函数”．例如，函数y=x²与y=-x²关于原点O互为“对称函数”．
（1）函数y=-x+1关于原点O的“对称函数”的函数解析式为
，函数y=（x-2）²-1关于原点O的“对称函数”的函数解析式为
；
（2）已知函数y=x²-2x与函数G关于点Q（0，1）互为“对称函数”，若函数y=x²-2x与函数G的函数值y都随自变量x的增大而减小，求x的取值范围；
（3）已知点A（0，1），点B（4，1），点C（2，0），二次函数y=ax²-2ax-3a（a＞0），与函数N关于点C互为“对称函数”，将二次函数y=ax²-2ax-3a（a＞0）与函数N的图象组成的图形记为W，若图形W与线段AB恰有2个公共点，直接写出a的取值范围．
组卷：684引用：3难度：0.1
解析
25．已知△ABC为等腰直角三角形，∠CAB=90°，点D为平面内的一动点，满足CD=CA，将线段AD绕A点按逆时针方向旋转90°得到线段AE，连接CE．

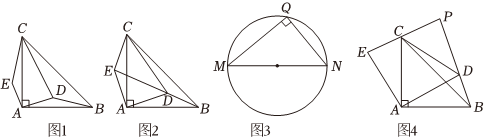
（1）当点D在△ABC内部时．①如图1，求证：△AEC≌△ADB；②如图2，当点E，D，B在同一直线上时，若
AB
=
2
10
，求CE的长；
（2）阅读材料：如图3，已知线段MN为定长，若以MN为斜边作Rt△MQN，其中∠Q=90°，根据直角三角形的性质“直角三角形斜边上的中线等于斜边的一半”，则以MN为斜边的直角三角形的直角顶点Q的轨迹是：以线段MN中点为圆心，
1
2
MN
长为半径的圆（M，N两点除外）．如图4，已知AB=6．若直线CE与直线BD相交于点P．点G为线段BC上的一动点，将线段AG绕点A按顺时针方向旋转90°得到AG'，连接PG'，求PG'长度的取值范围．
组卷：187引用：3难度：0.2
解析