2023年湖北省孝感市中考数学试卷

一、精心选一选（本大题共8小题，每小题3分，满分24分，在每小题给出的四个选项中只有一项是符合题目要求的．清在答题卡上把正确答案的代号涂黑）

• 1．-2的相反数为（　　）

  A．-2

  B．2

  C． - 1 2

  D． 1 2
  组卷：176引用：1难度：0.8

  解析

• 2．2023年全国普通高校毕业生规模预计达到1158万人，数11580000用科学记数法表示为（　　）

  A．1.158×107

  B．1.158×108

  C．1.158×103

  D．1158×104
  组卷：288引用：3难度：0.9

  解析

• 3．下列几何体中，三视图都是圆的是（　　）

  A．长方体

  B．圆柱

  C．圆锥

  D．球
  组卷：294引用：6难度：0.8

  解析

• 4．不等式组

  x - 1 ＜ 0

  x + 1 ＞ 0

  的解集为（　　）

  A．x＞-1

  B．x＜1

  C．-1＜x＜1

  D．无解
  组卷：396引用：5难度：0.5

  解析

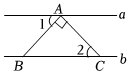• 5．如图，Rt△ABC的直角顶点A在直线a上，斜边BC在直线b上，若a∥b,∠1=55°，则∠2=（　　）

  A．55°

  B．45°

  C．35°

  D．25°
  组卷：728引用：11难度：0.7

  解析

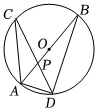• 6．如图，在⊙O中，直径AB与弦CD相交于点P，连接AC，AD，BD，若∠C=20°，∠BPC=70°，则∠ADC=（　　）

  A．70°

  B．60°

  C．50°

  D．40°
  组卷：2360引用：16难度：0.5

  解析

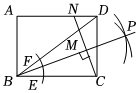• 7．如图，矩形ABCD中，AB=3，BC=4，以点B为圆心，适当长为半径画弧，分别交BC，BD于点E，F，再分别以点E，F为圆心，大于

  1

  2

  EF

  长为半径画弧交于点P，作射线BP，过点C作BP的垂线分别交BD，AD于点M，N，则CN的长为（　　）

  A． 10

  B． 11

  C． 2 3

  D．4
  组卷：2693引用：32难度：0.5

  解析

• 8．已知二次函数y=ax²+bx+c（a＜0）的图象与x轴的一个交点坐标为（-1，0），对称轴为直线x=1，下列结论中：①a-b+c=0；②若点（-3，y₁），（2，y₂），（4，y₃）均在该二次函数图象上，则y₁＜y₂＜y₃；③若m为任意实数，则am²+bm+c⩽-4a；④方程ax²+bx+c+1=0的两实数根为x₁，x₂，且x₁＜x₂，则x₁＜-1，x₂＞3．正确结论的序号为（　　）

  A．①②③

  B．①③④

  C．②③④

  D．①④
  组卷：1357引用：3难度：0.5

  解析

三、专心解一解（本大题共8小题，满分72分．请认真读题，冷静思考解答题应写出必要的文字说明、证明过程或演算步骤，请把解题过程写在答题卡相应题号的位置）

• 23．【问题呈现】
  △CAB和△CDE都是直角三角形，∠ACB=∠DCE=90°，CB=mCA，CE=mCD，连接AD，BE，探究AD，BE的位置关系．
  【问题探究】
  （1）如图1，当m=1时，直接写出AD，BE的位置关系：

  ．
  （2）如图2，当m≠1时，（1）中的结论是否成立？若成立，给出证明；若不成立，说明理由．
  【拓展应用】
  （3）当m=

  3

  ，AB=4

  7

  ，DE=4时，将△CDE绕点C旋转，使A，D，E三点恰好在同一直线上，求BE的长．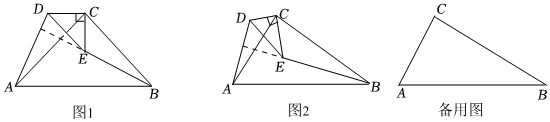
  
  组卷：3766引用：18难度：0.3

  解析

• 24．已知抛物线

  y

  =

  -

  1

  2

  x

  2

  +

  bx

  +

  c

  与x轴交于A，B（4，0）两点，与y轴交于点C（0，2）．点P为第一象限抛物线上的点，连接CA，CB，PB，PC．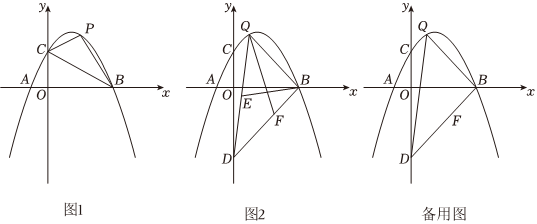
  
  （1）直接写出结果；b=

  ，c=

  ，点A的坐标为

  ，tan∠ABC=

  ；
  （2）如图1，当∠PCB=2∠OCA时，求点P的坐标；
  （3）如图2，点D在y轴负半轴上，OD=OB，点Q为抛物线上一点，∠QBD=90°．点E，F分别为△BDQ的边DQ，DB上的动点，且QE=DF，记BE+QF的最小值为m.
  ①求m的值；
  ②设△PCB的面积为S，若

  S

  =

  1

  4

  m

  2

  -

  k

  ，请直接写出k的取值范围．
  组卷：2256引用：6难度：0.1

  解析