当前位置：试卷中心 > 试卷详情

2022-2023学年黑龙江省齐齐哈尔市龙江县育英学校九年级（上）期中数学试卷

发布：2024/9/5 18:0:8

一、单项选择题（每小题3分，共计30分）

1．下列方程中，关于x的一元二次方程是（　　）
A．2x-3=x B．2x+3y=5 C．2x-x²=1 D．x+
1
x
=7
组卷：802引用：16难度：0.7
解析
2．下列食品标识中，既是轴对称图形又是中心对称图形的是（　　）
A．
绿色饮品 B．
绿色食品 C．
有机食品 D．
速冻食品
组卷：1741引用：32难度：0.8
解析
3．在平面直角坐标系中，将抛物线y=-x²先向右平移1个单位长度，再向下平移2个单位长度，得到的新抛物线的解析式为（　　）
A．y=-（x-1）²-2 B．y=-（x+1）²-2
C．y=-（x-1）²+2 D．y=-（x+1）²+2
组卷：303引用：7难度：0.8
解析
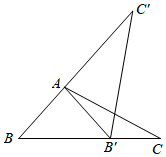4．如图，将△ABC绕点A逆时针旋转80°得到△AB′C′，若点B′恰好落到边BC上，则∠CB′C′的度数为（　　）
A．50° B．60° C．70° D．80°
组卷：1100引用：9难度：0.6
解析
5．当b+c=5时，关于x的一元二次方程3x²+bx-c=0的根的情况为（　　）
A．有两个相等的实数根 B．有两个不相等的实数根
C．没有实数根 D．以上情况都有可能
组卷：23引用：1难度：0.5
解析
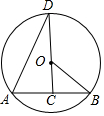6．已知，如图AB，AD是⊙O的弦，∠B=30°，点C在弦AB上，连接CO并延长交⊙O于点D，∠D=35°，则∠BAD的度数是（　　）
A．60° B．65° C．70° D．75°
组卷：327引用：3难度：0.8
解析
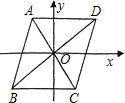7．如图，已知▱ABCD的两条对角线AC与BD交于平面直角坐标系的原点，点A的坐标为（-2，3），则点C的坐标为（　　）
A．（-3，2） B．（-2，-3） C．（3，-2） D．（2，-3）
组卷：529引用：58难度：0.9
解析
8．如图，在半径为
5
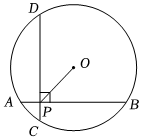的⊙O中，AB、CD是互相垂直的两条弦，垂足为P，且AB=CD=4，则OP的长为（　　）
A．1 B．
2
C．2 D．2
2
组卷：3559引用：19难度：0.9
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本题共计7小题，共计69分）

23．综合与实践
观察猜想：
（1）如图1，在△ABC和△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点D在线段AC上，连接BD，CE．则BD和CE的数量关系是
，∠ABD和∠ACE的关系是
．
探索证明：
（2）如图2和图3，将△ADE绕点A顺时针和逆时针旋转，其他条件与（1）相同，（1）中的结论是否成立？若成立，请选择一种情况证明；若不成立，请说明理由．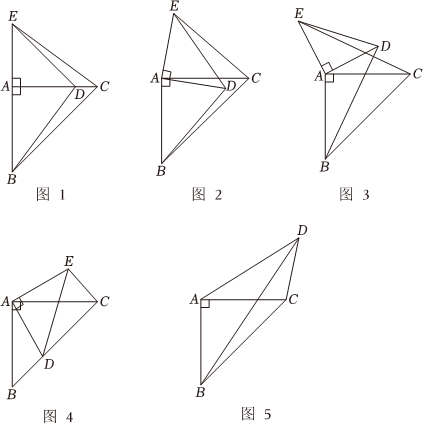

拓展延伸：
（3）如图4，若图2中的点D落在线段BC上，其他条件不变，则此时线段BD、DC、AD的关系是
．
（4）如图5，△ABC是等腰直角三角形，∠BAC=90°，点D为△ABC外一点，且∠ADC=45°，连接BD．若BD=9，CD=3，则AD的长为
．
组卷：110引用：1难度：0.3
解析
24．综合与探究
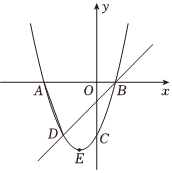
如图，已知抛物线y=x²+bx+c与x轴交于A、B两点，与y轴交于点C，顶点为点E，已知点B的坐标为（1，0），经过点B的直线与抛物线另一个交点D的坐标为（-2，-3），连接AD．
（1）求抛物线及直线BD的解析式；
（2）若点F在x轴上，则当EF+CF的值最小时，点F的坐标为
；
（3）若点P是抛物线上不与点D重合的一个动点，求当S_△ABP=
5
3
S_△ABD时点P的坐标；
（4）是否存在点M在抛物线上，点N在直线BD上，使得△DMN为等腰直角三角形？若存在，直接写出点N的坐标；若不存在，请说明理由．
组卷：101引用：3难度：0.1
解析