2023-2024学年江苏省苏州市常熟市昆承中学九年级(上)月考数学试卷(10月份)
发布:2024/9/8 10:0:8
一、选择题。(本大题共8小题,每小题3分,共24分)
-
1.下列方程是一元二次方程的是( )
组卷:310引用:9难度:0.8 -
2.若二次函数y=ax2的图象经过点P(4,3),则该图象必过点( )
组卷:103引用:1难度:0.6 -
3.用配方法解方程x2-4x+2=0时,配方后所得的方程是( )
组卷:106引用:7难度:0.9 -
4.一元二次方程x2-4x+5=0的根的情况是( )
组卷:1755引用:160难度:0.9 -
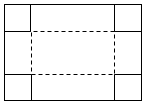 5.如图,把一块长为45cm,宽为25cm的矩形硬纸板的四角剪去四个相同的小正方形,然后把纸板沿虚线折起,做成一个无盖纸盒.若该无盖纸盒的底面积为625cm2,设剪去小正方形的边长为x cm,则可列方程为( )组卷:364引用:4难度:0.8
5.如图,把一块长为45cm,宽为25cm的矩形硬纸板的四角剪去四个相同的小正方形,然后把纸板沿虚线折起,做成一个无盖纸盒.若该无盖纸盒的底面积为625cm2,设剪去小正方形的边长为x cm,则可列方程为( )组卷:364引用:4难度:0.8 -
6.函数y=ax2+1和y=ax+a(a为常数,且a≠0),在同一平面直角坐标系中的大致图象可能是( )
组卷:1252引用:12难度:0.6 -
7.若a是方程x2-x-1=0的一个根,则-a3+2a+2022的值为( )
组卷:1452引用:5难度:0.5 -
8.如图1,在平行四边形ABCD中,点P沿A→B→C方向从点A移动到点C,设点P移动路程为x,线段AP的长为y,图2是点P运动时y随x变化的关系图象,则BC的长为( )
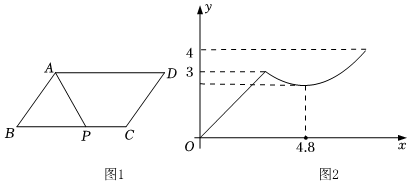 组卷:1552引用:16难度:0.5
组卷:1552引用:16难度:0.5
三、解答题。(共8题,82分)
-
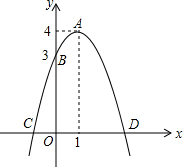 24.如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C,D两点.点P是x轴上的一个动点.
24.如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C,D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)当PA+PB的值最小时,求点P的坐标;
(3)抛物线上是否存在一点Q(Q与B不重合),使△CDQ的面积等于△BCD的面积?若存在,直接写出点Q的坐标;若不存在,请说明理由.组卷:2953引用:7难度:0.4 -
25.如图,抛物线y=-
x2+mx+n与x轴交于A、B两点(A在B的左侧),与y轴交于点C,已知A(-1,0),AB=5.12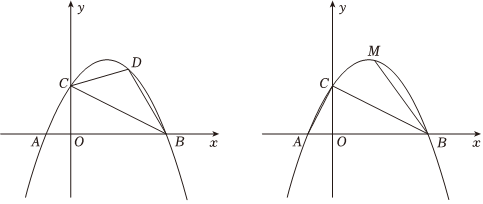
(1)求抛物线的解析式;
(2)点D是第一象限抛物线上的一个动点,当点D在运动过程中,求△CBD的面积的最大值,并写出此时点D的坐标;
(3)在第一象限的抛物线上是否存在点M,使得∠ACO=∠CBM,若存在,求出点M的坐标;若不存在,请说明理由.组卷:1422引用:5难度:0.1


