2022-2023学年北京师大亚太实验学校九年级（上）期中数学试卷

一、选择题（本题共16分，每小题2分）

• 1．抛物线y=-（x+1）²-2的对称轴是（　　）

  A．x=1

  B．x=-1

  C．x=2

  D．x=-2
  组卷：610引用：6难度：0.8

  解析

• 2．如图，不是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：2引用：3难度：0.9

  解析

• 3．若方程（m-1）x^|m|+1-2x=3是关于x的一元二次方程，则m的值为（　　）

  A．1

  B．-1

  C．±1

  D．不存在
  组卷：838引用：10难度：0.8

  解析

• 4．方程x²-3x+1=0的根的情况是（　　）

  A．有两个相等实数根	B．有两个不相等实数根
  C．没有实数根	D．无法判断
  组卷：672引用：14难度：0.8

  解析

• 5．将抛物线y=2x²向左平移1个单位，再向上平移3个单位得到的表达式是（　　）

  A．y=2（x-1）2-3	B．y=2（x+1）2-3
  C．y=2（x-1）2+3	D．y=2（x+1）2+3
  组卷：151引用：5难度：0.8

  解析

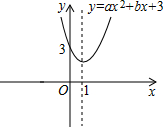• 6．如图，抛物线y=ax²+bx+3（a≠0）的对称轴为直线x=1，如果关于x的方程ax²+bx-8=0（a≠0）的一个根为4，那么该方程的另一个根为（　　）

  A．-4

  B．-2

  C．1

  D．3
  组卷：1613引用：22难度：0.7

  解析

• 7．在平面直角坐标系xOy中，点（-1，y₁），（2，y₂），（4，y₃）在抛物线y=ax²-2ax+c上，当a＞0时，下列说法一定正确的是（　　）

  A．若y1y2＜0，则y3＞0	B．若y2y3＞0，则y1＜0
  C．若y1y3＜0，则y2＞0	D．若y1y2y3=0，则y2=0
  组卷：1661引用：15难度：0.5

  解析

• 8．在平面直角坐标系xOy中，开口向下的抛物线y=ax²+bx+c的一部分图象如图所示，它与x轴交于A（1，0），与y轴交于点B（0，3），则a的取值范围是（　　）

  A．a＜0

  B．-3＜a＜0

  C．a＜ - 3 2

  D． - 9 2 ＜a＜ - 3 2
  组卷：1262引用：13难度：0.7

  解析

二、填空题（本题共16分，每小题2分）

• 9．请你写出一个二次函数，其图象满足条件：①开口向下；②图象过原点，此二次函数的解析式可以是

  ．
  组卷：98引用：3难度：0.9

  解析

三、解答题（本题共68分，第17题每小题6分，第18-23题，每题5分，第24-26题，每题6分，第27-28题，每题7分）解答应写出文字说明、演算步骤或证明过程.

• 27．在△ABC中，AD为∠BAC的平分线，E为边AC中点，线段EA绕点E旋转得到线段EF（点F是点A的对应点），连接AF，直线EF交直线AB于点G．
  （1）如图1，当△ABC为等边三角形且点G在边AB上时，若∠FAD=20°，则∠AGE=

  ；
  （2）如图2，点G在边AB上，AD与EG交于点O，OG=OA，AG=AD，求证：GF=FD．
  （3）如图3，若∠BAC＞60°，过点C作CM⊥直线AD于M，连接MF，当MF=AE时，请直接写出∠FAC与∠DAC的数量关系．
  
  组卷：201引用：2难度：0.1

  解析

• 28．在平面直角坐标系xOy中，对于点A和线段MN，如果点A，O，M，N按逆时针方向排列构成菱形AOMN，且∠AOM=α，则称线段MN是点A的“α-相关线段”．例如，图1中线段MN是点A的“30°-相关线段”．
  （1）已知点A的坐标是（0，2）．
  ①在图2中画出点A的“30°-相关线段”MN，并直接写出点M和点N的坐标；
  ②若点A的“α-相关线段”经过点（

  3

  ，1），求α的值；
  （2）若存在α，β（α≠β）使得点P的“α-相关线段”和“β-相关线段”都经过点（0，4），记PO=t,直接写出t的取值范围．
  
  组卷：1206引用：7难度：0.1

  解析