2022-2023学年山东省泰安市宁阳县九年级(上)期中数学试卷(五四学制)
发布:2024/9/25 15:0:1
一、单选题(每题4分,共计48分)
-
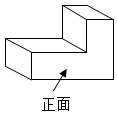 1.如图所示的几何体,其俯视图是( )组卷:256引用:8难度:0.8
1.如图所示的几何体,其俯视图是( )组卷:256引用:8难度:0.8 -
2.若反比例函数y=
(k≠0)的图象经过点P(-2,3),则该函数的图象不经过的点是( )kx组卷:865引用:84难度:0.9 -
3.如果函数y=x2m-1为反比例函数,则m的值是( )
组卷:456引用:25难度:0.9 -
4.若A(-3,y1)、B(-2,y2)、C(1,y3)三点都在函数y=-
的图象上,则y1,y2,y3的大小关系是( )1x组卷:907引用:6难度:0.6 -
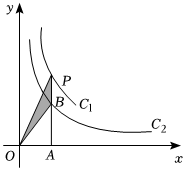 5.如图,两个反比例函数y1=和y2=4x在第一象限内的图象分别是C1和C2,设点P在C1上,PA⊥x轴于点A,交C2于点B,则△POB的面积为( )2x组卷:4488引用:14难度:0.5
5.如图,两个反比例函数y1=和y2=4x在第一象限内的图象分别是C1和C2,设点P在C1上,PA⊥x轴于点A,交C2于点B,则△POB的面积为( )2x组卷:4488引用:14难度:0.5 -
6.反比例函数y=-
与一次函数y=kx-3在同一坐标系中的大致图象可能是( )kx组卷:1221引用:8难度:0.6 -
7.根据如图所示的程序计算函数y的值,若输入的x值为3或-4时,输出的y值互为相反数,则b等于( )
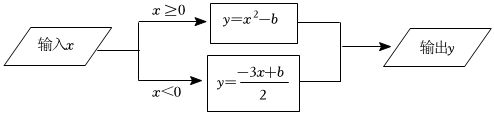 组卷:1160引用:8难度:0.7
组卷:1160引用:8难度:0.7 -
8.把二次函数y=3x2的图象先向左平移3个单位长度,再向下平移5个单位长度,得到的图象的解析式为( )
组卷:195引用:6难度:0.6
三、解答题(共78分)
-
 24.二次函数y=ax2+bx+4(a≠0)的图象经过点A(-4,0),B(1,0),与y轴交于点C,点P为第二象限内抛物线上一点,连接BP、AC,交于点Q,过点P作PD⊥x轴于点D.
24.二次函数y=ax2+bx+4(a≠0)的图象经过点A(-4,0),B(1,0),与y轴交于点C,点P为第二象限内抛物线上一点,连接BP、AC,交于点Q,过点P作PD⊥x轴于点D.
(1)求二次函数的表达式;
(2)在对称轴上是否存在一个点M,使MB+MC的和最小,存在的话,请求出点M的坐标.不存在的话请说明理由.
(3)连接BC,当∠DPB=2∠BCO时,求直线BP的表达式.组卷:123引用:1难度:0.2 -
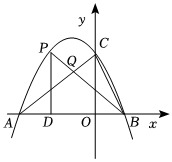
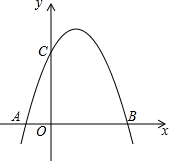 25.如图,是将抛物线y=-x2平移后得到的抛物线,其对称轴为直线x=1,与x轴的一个交点为A(-1,0),另一个交点为B,与y轴的交点为C.
25.如图,是将抛物线y=-x2平移后得到的抛物线,其对称轴为直线x=1,与x轴的一个交点为A(-1,0),另一个交点为B,与y轴的交点为C.
(1)求抛物线的函数表达式;
(2)若点N为抛物线上一点,且BC⊥NC,求点N的坐标;
(3)点P是抛物线上一点,点Q是一次函数y=x+32的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标;若不存在,说明理由.32组卷:4082引用:14难度:0.3


