2020-2021学年湖北省武汉市东西湖区九年级（上）期中数学试卷

一、选一选，比比谁细心（共十题：共30分）

• 1．下列函数中，是二次函数的是（　　）

  A． y = 1 x 2 - x	B．y=x2-（x-1）2
  C． y = x 2 - 2 x 2	D． y = x 2 + 1 x
  组卷：318引用：6难度：0.9

  解析

• 2．下列图案中既是中心对称图形，又是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：73引用：7难度：0.9

  解析

• 3．抛物线y=x²-mx-m²+1的图象过原点，则m为（　　）

  A．0

  B．1

  C．-1

  D．±1
  组卷：1545引用：53难度：0.7

  解析

• 4．抛物线y=2x²向下平移一个单位，得到的抛物线的解析式为（　　）

  A．y=2x2+1

  B．y=2x2-1

  C．y=2（x+1）2

  D．y=2（x-1）2
  组卷：24引用：2难度：0.5

  解析

• 5．平面直角坐标系中，与点（-2，1）关于原点对称的点的坐标是（　　）

  A．（-2，1）

  B．（-2，-1）

  C．（2，-1）

  D．（2，1）
  组卷：134引用：6难度：0.9

  解析

• 6．把如图所示的五角星图案，绕着它的中心旋转，若旋转后的五角星能与自身重合．则旋转角至少为（　　）

  A．30°

  B．45°

  C．60°

  D．72°
  组卷：686引用：13难度：0.9

  解析

• 7．关于x的一元二次方程（a-1）x²+x+a²-1=0的一个根是0，则a的值为（　　）

  A．1

  B．-1

  C．1或-1

  D． 1 2
  组卷：22008引用：347难度：0.9

  解析

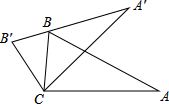• 8．如图，将△ABC绕顶点C逆时针旋转得到△A′B′C′，且点B刚好落在A′B′上，若∠A=25°，∠BCA′=45°，则∠A′BA等于（　　）

  A．30°

  B．35°

  C．40°

  D．45°
  组卷：2132引用：21难度：0.9

  解析

三、解一解，看看谁更棒（共八题：共72分）

• 23．定义：如图1，在△ABC中，把AB绕点A顺时针旋转α（0°＜α＜180°）得到AB'，把AC绕点A逆时针旋转β得到AC'，连接B'C'．当α+β=180°时，我们称△AB'C'是△ABC的“旋补三角形”，△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”，点A叫做“旋补中心”．
  （1）在图2中，△AB'C'是△ABC的“旋补三角形”，AD是△ABC的“旋补中线”，若△ABC为等边三角形，则AD与BC的数量关系为：AD=

  BC．
  （2）在图1中，当△ABC为任意三角形时，猜想AD与BC的数量关系，并给予证明．
  （3）如图3，在四边形ABCD中，∠B=90°，∠A=150°，BC=12，AB=2

  3

  ，AD=6．若四边形内部恰好存在一点P，使△PAB是△PDC的“旋补三角形”，请直接写出△PDC的“旋补中线”长是

  ．
  
  组卷：175引用：3难度：0.3

  解析

• 24．如图，已知抛物线y=-x²+mx+m-2的顶点为A，且经过点B（3，-3）．
  （1）求顶点A的坐标；
  （2）在对称轴左侧的抛物线上存在一点P，使得∠PAB=45°，求点P坐标；
  （3）如图（2），将原抛物线沿射线OA方向进行平移得到新的抛物线，新抛物线与射线OA交于C，D两点，请问：在抛物线平移的过程中，线段CD的长度是否为定值？若是，请求出这个定值；若不是，请说明理由．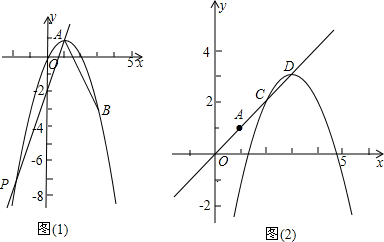
  
  组卷：719引用：5难度：0.3

  解析