2023-2024学年福建省厦门市思明区双十中学海沧附属学校八年级（上）适应性数学试卷（10月份）

一、选择题（每题3分，共30分）

• 1．第19届杭州亚运会刚刚落下帷幕，在以下给出的运动图片中，属于轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：401引用：25难度：0.9

  解析

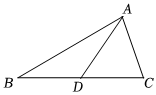• 2．如图，AD是△ABC的中线，则下列结论正确的是（　　）

  A．AB=AC

  B．BD=CD

  C．BD=AD

  D．AC=AD
  组卷：1066引用：11难度：0.9

  解析

• 3．下列生活实物中，没有应用到三角形的稳定性的是（　　）

  A． 太阳能热水器	B． 篮球架
  C． 三脚架	D． 活动衣架
  组卷：668引用：26难度：0.7

  解析

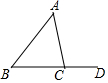• 4．如图，在△ABC中，∠A=55°，∠B=45°，那么∠ACD的度数为（　　）

  A．110

  B．100

  C．55

  D．45
  组卷：1106引用：30难度：0.9

  解析

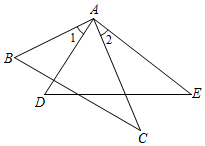• 5．如图，已知AE=AC，∠C=∠E，下列条件中，无法判定△ABC≌△ADE的是（　　）

  A．∠B=∠D

  B．BC=DE

  C．∠1=∠2

  D．AB=AD
  组卷：8127引用：52难度：0.7

  解析

• 6．如图，在△ABC中，分别以点A，B为圆心，大于

  1

  2

  AB长为半径画弧，两弧分别交于点D，E，则直线DE是（　　）

  A．∠A的平分线	B．AC边的中线
  C．BC边的高线	D．AB边的垂直平分线
  组卷：1311引用：11难度：0.9

  解析

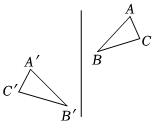• 7．把一个图形先沿着一条直线进行轴对称变换，再沿着与这条直线平行的方向平移，我们把这样的图形变换叫做滑动对称变换．结合轴对称变换和平移变换的有关性质，你认为在滑动对称变换过程中，两个对应三角形（如图）的对应点所具有的性质是（　　）

  A．对应点连线与对称轴垂直

  B．对应点连线被对称轴平分

  C．对应点连线都相等

  D．对应点连线互相平行
  组卷：523引用：9难度：0.7

  解析

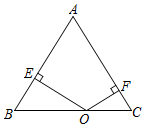• 8．如图，△ABC是等腰三角形，点O是底边BC上任意一点，OE、OF分别与两边垂直，等腰三角形ABC的腰长为5，面积为12，则OE+OF的值为（　　）

  A．4

  B． 24 5

  C．15

  D．8
  组卷：500引用：8难度：0.6

  解析

三、解答题（本大题共8小题，共72分）

• 23．新定义：我们把两个面积相等但不全等的三角形叫做偏等积三角形，
  初步尝试
  （1）如图1，在△ABC中，∠ACB=90°，AC=BC=6，P为AC上一点，当AP的长为

  时，△ABP与△CBP为偏等积三角形；
  理解运用
  （2）如图2，△ABD与△ACD为偏等积三角形，AB=2，AC=4，且线段AD的长度为正整数，过点C作CE平行AB，交AD的延长线于点E，求AE的长；
  综合应用
  （3）如图3，已知四边形ADEB，△ACB、△DCE是等腰直角三角形，∠ACB=∠DCE=90°（0＜∠BCE＜90°），则△ACD与△BCE是偏等积三角形吗？请说明理由．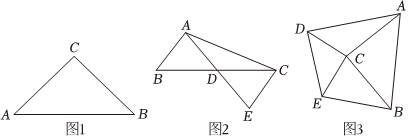
  
  组卷：180引用：5难度：0.4

  解析

• 24．在平面直角坐标系中，点A（0，a），B（b,0），a、b满足（a-2）²+|b-4|=0，点P在第一象限，PA=PB，且PA⊥PB．
  （1）如图1，点P的坐标为

  ；
  （2）如图2，若A点运动到A₁位置，B点运动到B₁位置，保持PA₁⊥PB₁，求OB₁-OA₁的值；
  （3）如图3，若Q是线段AB上一点，C为AQ中点，作PR=PQ，PR⊥PQ，连BR，判定线段BR与PC的关系，并加以证明．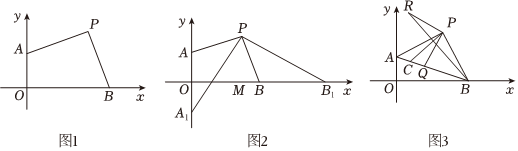
  
  组卷：106引用：4难度：0.5

  解析