2022-2023学年云南省昭通市镇雄县八年级（上）第三次月考数学试卷

一、选择题（本大题共12小题，每小题只有一个正确选项，每小题3分，共36分）

• 1．计算（-2）⁰的结果是（　　）

  A．1

  B．-2

  C．0

  D．-1
  组卷：344引用：9难度：0.8

  解析

• 2．下列四个冬奥会图标中，可以看作轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：1引用：1难度：0.8

  解析

• 3．下列长度的三条线段，能组成三角形的是（　　）

  A．4，4，9

  B．5，6，11

  C．5，9，9

  D．3，4，8
  组卷：5引用：1难度：0.7

  解析

• 4．如图，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么，最省事的方法是（　　）

  A．带①去	B．带②去
  C．带③去	D．带①去和带②去
  组卷：1633引用：18难度：0.8

  解析

• 5．下列运算正确的是（　　）

  A．2a-a=2	B．（-a2）3=-a6
  C．x6÷x3=x2	D．（x+y）2=x2+y2
  组卷：6引用：2难度：0.9

  解析

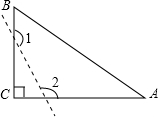• 6．如图，已知△ABC中，∠C=90°，若沿图中虚线剪去∠C，则∠1+∠2等于（　　）

  A．90°

  B．135°

  C．270°

  D．315°
  组卷：1850引用：33难度：0.9

  解析

• 7．下列各式从左到右的变形中，属于因式分解的是（　　）

  A．10a2-5a=5a（2a-1）

  B．x2+2x-1=（x-1）2

  C．x2-4+2x=（x+2）（x-2）+2x

  D．（x+2）（x-1）=x2+x-2
  组卷：8引用：1难度：0.8

  解析

• 8．若a²-（m+1）a+36是完全平方式，则m的值为（　　）

  A．-13

  B．-11或13

  C．11或-13

  D．11
  组卷：9引用：1难度：0.7

  解析

三、解答题（本大题共6小题，共46分）

• 23．阅读材料：
  若x²-2xy+2y²-6y+9=0，求x,y的值．
  解：∵x²-2xy+2y²-6y+9=0，
  ∴（x²-2xy+y²）+（y²-6y+9）=0，
  ∴（x-y）²+（y-3）²=0，
  ∴x-y=0，y-3=0，
  ∴x=y=3．
  根据上述材料，探究下列问题：
  （1）若△ABC的三边长a,b,c均为正整数，且满足a²+b²-8a-10b+41=0，求△ABC周长的最小值；
  （2）若△ABC的三边长为a,b,c,且满足a²+b²+2c（c-a-b）=0，试判断△ABC是什么形状的三角形，并说明理由．
  组卷：48引用：1难度：0.7

  解析

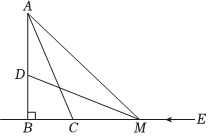• 24．如图，在△ABC中，∠ABC=90°，AB=12，BC=5，AC=13，点D在边AB上，且BD=BC，点E在边BC的延长线上，且CE=15，动点M从点E出发，沿射线EB以每秒2个单位长度的速度运动，运动时间为t s.
  （1）用含t的代数式表示BM的长；
  （2）在点M的运动过程中，是否存在某一时刻，使得△MBD与△ABC全等？若存在，请求出对应的t的值；若不存在，请说明理由；
  （3）在点M的运动过程中，当△ACM是以AC为腰的等腰三角形时，直接写出满足条件的t的值．
  组卷：54引用：2难度：0.3

  解析