2023-2024学年湖北省黄石市四校联考八年级（上）第一次月考数学试卷
发布：2024/9/14 10:0:8
一、单选题（本题共10小题，每题3分，共30分）
-
1．下列各组长度的线段能构成三角形的是（ ）
组卷：197引用：3难度：0.7 -
2．若一个正多边形的内角和为1800°，则这个正多边形的一个外角为（ ）
组卷：107引用：8难度：0.9 -
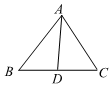3．如图，AD为△ABC的中线，AD=3，AC=4，则AB的长的取值范围是（ ）组卷：336引用：4难度：0.5 -
4．如图，在锐角△ABC中，CD，BE分别是AB，AC边上的高，且CD，BE相交于一点P，若∠A=50°，则∠BPC=（ ）组卷：1960引用：100难度：0.9 -
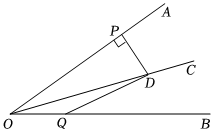5．如图．射线OC是∠AOB的平分线，D是射线OC上一点，DP⊥OA于点P，点Q是射线OB上一点，若OQ=3，且△ODQ的面积是6，则DP长为（ ）组卷：47引用：4难度：0.5 -
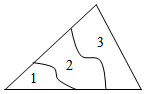6．如图，一块三角形的玻璃碎成3块（图中所标1、2、3），小华带第3块碎片去玻璃店，购买形状相同、大小相等的新玻璃，这是利用三角形全等中的（ ）组卷：863引用：11难度：0.7 -
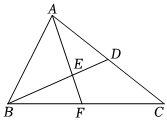7．如图，BD是△ABC的中线，点E为BD上一点，BE=2ED，连接AE并延长，交BC于点F，若△ABC的面积是24cm2，则△AED的面积是（ ）组卷：385引用：5难度：0.5 -
8．在平面直角坐标系中，将点A（m,n+2）先向左平移3个单位，再向上平移2个单位，得到点A′，若点A'位于第二象限，则m、n的取值范围分别是（ ）
组卷：529引用：6难度：0.5
三、解答题（本题共8小题，共72分）
-
23．为了进一步探究三角形中线的作用，数学兴趣小组合作交流时，小丽在组内做了如下尝试：如图1，在△ABC中，AD是BC边上的中线，延长AD到M，使DM=AD，连接BM．
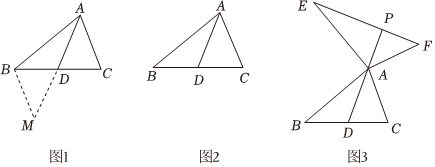
【探究发现】（1）图1中AC与BM的数量关系是 ，位置关系是 ；
【初步应用】（2）如图2，在△ABC中，若AB=12，AC=8，求BC边上的中线AD的取值范围；
【探究提升】（3）如图3，AD是△ABC的中线，过点A分别向外作AE⊥AB、AF⊥AC，使得AE=AB，AF=AC，延长DA交EF于点P，判断线段EF与AD的数量关系和位置关系，请说明理由．组卷：360引用：6难度：0.2 -
24．如图，在平面直角坐标系内，有一个等腰Rt△ABC，∠ABC=90°，AB=BC．
（1）如图1，点A（-4，0），点B（0，-1），点C的坐标为．
（2）如图2，点A（-4，0），点B在y轴负半轴上，点C在第一象限，过点C作CH垂直于x轴于点H，则CH+OB的值为．
（3）如图3，点B与原点重合，点A在x轴负半轴上，点C在y轴正半轴上，点D为x轴正半轴上一点，点M为线段AD中点，在y轴正半轴上取点E，使OE=OD，过点D作FD⊥CD，交EM的延长线于点F，请补全图形，判断CD与DF的数量关系，并证明你的结论．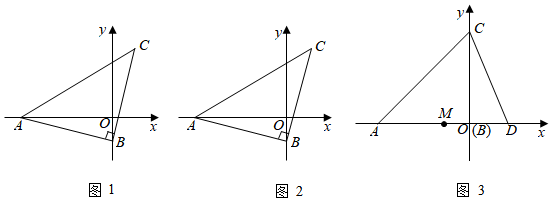
组卷：442引用：5难度：0.1
