2022-2023学年广东省惠州市惠阳区良井中学九年级(上)月考数学试卷(10月份)
发布:2024/8/11 14:0:1
一、选择题(共10题,共30分)
-
1.已知圆锥的母线长为5cm,底面半径为3cm,则圆锥的表面积为( )
组卷:87引用:33难度:0.7 -
2.抛物线y=(x-2)2-1可以由抛物线y=x2平移而得到,下列平移正确的是( )
组卷:3860引用:41难度:0.9 -
3.某种药品原来售价200元,连续两次降价后售价为162元,若每次下降的百分率相同,则这个百分率是( )
组卷:10引用:2难度:0.5 -
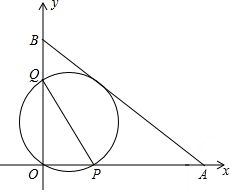 4.如图,A(8,0)、B(0,6)分别是平面直角坐标系xOy坐标轴上的点,经过点O且与AB相切的动圆与x轴、y轴分别相交于点P、Q,则线段PQ长度的最小值是( )组卷:1525引用:5难度:0.5
4.如图,A(8,0)、B(0,6)分别是平面直角坐标系xOy坐标轴上的点,经过点O且与AB相切的动圆与x轴、y轴分别相交于点P、Q,则线段PQ长度的最小值是( )组卷:1525引用:5难度:0.5 -
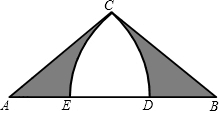 5.如图,在△ABC中,AC=BC=,∠ACB=90°,分别以点A和点B为圆心,以AC的长为半径画弧交AB于D,E两点,则阴影部分的面积是( )2组卷:587引用:2难度:0.6
5.如图,在△ABC中,AC=BC=,∠ACB=90°,分别以点A和点B为圆心,以AC的长为半径画弧交AB于D,E两点,则阴影部分的面积是( )2组卷:587引用:2难度:0.6 -
6.如图,在△ABC中,∠AOB=125°,把△ABC剪成三部分,边AB、BC、AC放在同一直线上,点O都落在直线MN上,且S△BCO:S△CAO:S△ABO=BC:CA:AB,则∠ACB的度数为( )
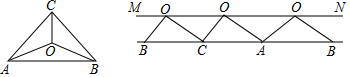 组卷:294引用:2难度:0.6
组卷:294引用:2难度:0.6 -
7.已知一元二次方程x2+x-1=0,嘉淇在探究该方程时,得到以下结论:
①该方程有两个不相等的实数根;②该方程有一个根为1;③该方程的根是整数;④该方程有一个根小于-1.则其中正确结论的序号为( )组卷:285引用:2难度:0.5 -
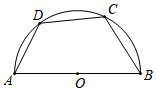 8.如图,四边形ABCD是半圆的内接四边形,AB是直径,=ˆDC.若∠C=110°,则∠ABC的度数等于( )ˆCB组卷:4657引用:34难度:0.7
8.如图,四边形ABCD是半圆的内接四边形,AB是直径,=ˆDC.若∠C=110°,则∠ABC的度数等于( )ˆCB组卷:4657引用:34难度:0.7
三、解答题(共8题,共62分)
-
24.小华同学对图形旋转前后的线段之间、角之间的关系进行了拓展探究.
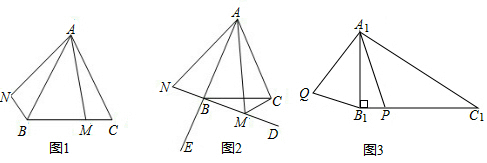
(一)猜测探究
在△ABC中,AB=AC,M是平面内任意一点,将线段AM绕点A按顺时针方向旋转与∠BAC相等的角度,得到线段AN,连接NB.
(1)如图1,若M是线段BC上的任意一点,请直接写出∠NAB与∠MAC的数量关系是,NB与MC的数量关系是;
(2)如图2,点E是AB延长线上点,若M是∠CBE内部射线BD上任意一点,连接MC,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由.
(二)拓展应用
如图3,在△A1B1C1中,A1B1=8,∠A1B1C1=90°,∠C1=30°,P是B1C1上的任意点,连接A1P,将A1P绕点A1按顺时针方向旋转60°,得到线段A1Q,连接B1Q.求线段B1Q长度的最小值.组卷:1727引用:4难度:0.3 -
25.如图①,在矩形ABCD中,动点P从A出发,以相同的速度,沿A→B→C→D→A方向运动到点A处停止.设点P运动的路程为x,△PAB面积为y,y与x的函数图象如图②所示.
(1)矩形ABCD的面积为;
(2)如图③,若点P沿AB边向点B以每秒1个单位的速度移动,同时,点Q从点B出发沿BC边向点C以每秒2个单位的速度移动.如果P、Q两点在分别到达B、C两点后就停止移动,回答下列问题:
①当运动开始秒时,试判断△DPQ的形状;32
②在运动过程中,是否存在这样的时刻,使以Q为圆心,PQ的长为半径的圆与矩形ABCD的对角线AC相切,若存在,求出运动时间;若不存在,请说明理由.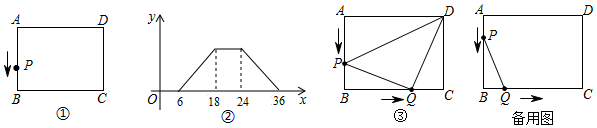 组卷:1015引用:3难度:0.1
组卷:1015引用:3难度:0.1


