当前位置：试卷中心 > 试卷详情

2022-2023学年辽宁省大连市庄河七中九年级（上）期中数学试卷

发布：2024/9/8 13:0:8

1．下列方程是关于x的一元二次方程的是（　　）
A．
x
2
+
1
x
-
2
=
0
B．2x=6x² C．2x+3=0 D．x²-y²=0
组卷：253引用：11难度：0.7
解析
2．下列图案是一些电视台的台标，是中心对称图形的是（　　）
A． B． C． D．
组卷：90引用：3难度：0.9
解析
3．点P（2，-1）关于原点对称的点P′的坐标是（　　）
A．（-2，1） B．（-2，-1） C．（-1，2） D．（1，-2）
组卷：1156引用：25难度：0.7
解析
4．下列方程没有实数根的是（　　）
A．x²-x-1=0 B．x²-6x+5=0 C．x²-3
2
x+3=0 D．x²+2x+2=0
组卷：365引用：3难度：0.8
解析
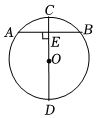5．如图，在⊙O中，CD是直径，AB是弦，AB⊥CD于E，AB=8，OD=5，则CE的长为（　　）
A．4 B．2 C．
2
D．1
组卷：349引用：5难度：0.7
解析
6．已知圆锥的底面半径为5cm,母线长为13cm,则这个圆锥的侧面积是（　　）
A．60πcm² B．65πcm² C．120πcm² D．130πcm²
组卷：1551引用：20难度：0.9
解析
7．将抛物线y=2（x-4）²-1先向左平移4个单位长度，再向上平移2个单位长度，平移后所得抛物线的解析式为（　　）
A．y=2x²+1 B．y=2x²-3
C．y=2（x-8）²+1 D．y=2（x-8）²-3
组卷：3236引用：54难度：0.7
解析
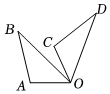8．如图，将△AOB绕着点O顺时针旋转，得△COD，若∠AOB=45°，∠AOD=110°，则旋转角度数是（　　）
A．45° B．55° C．65° D．110°
组卷：444引用：6难度：0.7
解析

25．已知，在正方形ABCD中，对角线AC与BD相交于点O．
（1）如图1，将线段CO绕点C顺时针旋转90°得到CE，连接BE交CO于点F，求证：BF=EF．
（2）如图2，若CD=4，点P是CD边上的点，且CP=1，连接OP，将线段OP绕点P顺时针旋转90°得到PH，连接BH交CO于点G．求OG的长．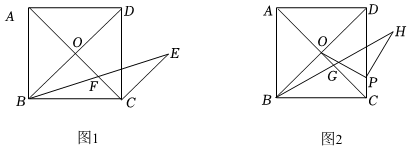
组卷：362引用：3难度：0.1
解析
26．如图，抛物线：y=ax²+bx+c与x轴交于A（1，0）、B（-3，0）两点，与y轴交于点C（0，-2）．
（1）求抛物线的解析式；
（2）动点P在抛物线：y=ax²+bx+c上移动，点Q在直线l：x=-4上移动，在运动过程中，是否存在△PAQ是以点P为直角顶点的等腰直角三角形？若存在，求出符合条件的点P的坐标；若不存在，请说明理由．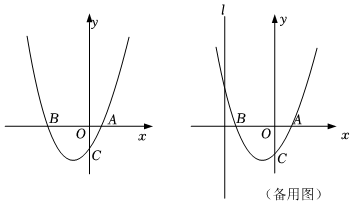
组卷：351引用：2难度：0.2
解析