2023-2024学年江西省南昌一中教育集团八年级（上）期中数学试卷

一、选择题（本大题共6小题，每小题3分，共18分）

• 1．“致中和，天地位焉，万物育焉．”对称美是我国古人和谐平衡思想的体现，常被用于建筑、器物、绘画、标识等作品的设计上，使对称美惊艳了千年的时光．下列大学的校徽图案是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：320引用：18难度：0.9

  解析

• 2．若正多边形的一个外角是60°，则这个正多边形的边数是（　　）

  A．4

  B．5

  C．6

  D．7
  组卷：2329引用：23难度：0.8

  解析

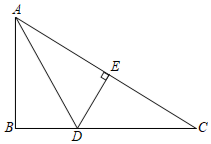• 3．如图，在Rt△ABC中，∠B=90°，AD平分∠BAC，交BC于点D，DE⊥AC，垂足为点E，若BD=1，则DE的长为（　　）

  A． 1 2

  B．1

  C．2

  D．6
  组卷：960引用：9难度：0.8

  解析

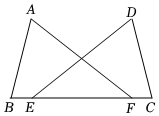• 4．如图，点E、点F在BC上，BE=CF，∠B=∠C，添加一个条件，不能证明△ABF≌△DCE的是（　　）

  A．∠A=∠D

  B．∠AFB=∠DEC

  C．AB=DC

  D．AF=DE
  组卷：3446引用：45难度：0.6

  解析

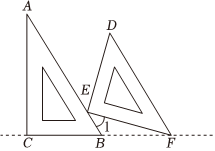• 5．将一副直角三角尺按如图摆放在同一平面内，直角顶点E在斜边AB上，且点F在CB的延长线上，已知∠A=30°，∠D=45°，当∠1=45°时，∠BFD的度数是（　　）

  A．45°

  B．60°

  C．70°

  D．75°
  组卷：967引用：7难度：0.5

  解析

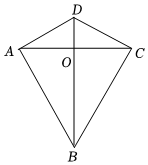• 6．两组邻边分别相等的四边形叫做“筝形”．如图，四边形ABCD是一个筝形，其中AD=CD，AB=CB，AC、BD交于点O．詹姆斯在探究筝形的性质时，得到如下结论：①AC⊥BD；②AO=CO=

  1

  2

  AC；③△ABD≌△CBD；④四边形ABCD的面积=AC•BD．其中正确的结论有（　　）

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：332引用：5难度：0.6

  解析

二、填空题（本大题共6小题，每小题3分，共18分）

• 7．平面直角坐标系中，点A（2，3）关于x轴的对称的点的坐标是

  ．
  组卷：1397引用：34难度：0.9

  解析

五、解答题（本大题共2小题，每小题9分，共18分）

• 22．如图，△ABC中，∠ACB=90°，AC=6cm,BC=8cm.点P从A点出发沿A-C-B路径向终点运动，终点为B点；点Q从B点出发沿B-C-A路径向终点运动，终点为A点．点P和Q分别以1cm/s和x cm/s的运动速度同时开始运动，两点都要到相应的终点时才能停止运动，在某时刻，分别过P和Q作PE⊥l于E，QF⊥l于F
  （1）如图1，当x=2时，设点P运动时间为t s,当点P在AC上，点Q在BC上时，
  ①用含t的式子表示CP和CQ，则CP=

  cm,CQ=

  cm；
  ②当t=2时，△PEC与△QFC全等吗？并说明理由；
  （2）请问：当x=3时，△PEC与△QFC有没有可能全等？若能，直接写出符合条件的t值：若不能，请说明理由．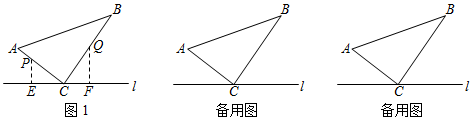
  
  组卷：1042引用：13难度：0.3

  解析

六、解答题（本大题共12分）

• 23．全等三角形是研究图形性质的主要工具，以此为基础，我们又探索出一些轴对称图形的性质与判定．通过寻找或构造轴对称图形，能运用其性质及判定为解题服务．
  
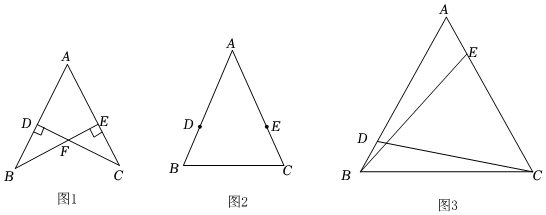
  （1）如图1，BE⊥AC，CD⊥AB，BD=CE，BE与CD相交于点F．
  ①求证：BE=CD；②连接AF，求证：AF平分∠BAC．
  （2）如图2，在△ABC中，AB=AC，点D、E分别在AB、AC上，且BD=CE．请你只用无刻度的直尺画出∠BAC的平分线．（不写画法，保留画图痕迹）．
  （3）如图3，在△ABC中，仍然有条件“AB=AC，点D，E分别在AB和AC上”．若∠ADC+∠AEB=180°，则CD与BE是否仍相等？为什么？
  组卷：228引用：2难度：0.3

  解析