2021-2022学年广东省广州市番禺区桥兴中学九年级(上)月考数学试卷(10月份)
发布:2024/8/21 3:0:1
一、选择题(本大题共10小题,每小题3分,共30分)
-
1.方程(a-2)x2+x+1=0是关于x的一元二次方程,则a的取值范围是( )
组卷:1328引用:7难度:0.8 -
2.二次函数y=2(x-3)2-6( )
组卷:885引用:12难度:0.9 -
3.抛物线y=(x-2)2+3的顶点坐标是( )
组卷:962引用:155难度:0.9 -
4.用配方法解一元二次方程x2-4x-9=0,可变形为( )
组卷:2548引用:25难度:0.7 -
5.二次函数y=-x2+1的图象与x轴交于A、B两点,与y轴交于点C,下列说法错误的是( )
组卷:1417引用:23难度:0.9 -
6.抛物线y=x2+4x+a2+5(a是常数)的顶点在( )
组卷:2233引用:6难度:0.8 -
7.直线y1=x+1与抛物线y2=-x2+3的图象如图,当y1>y2时,x的取值范围为( )
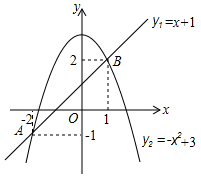 组卷:2109引用:17难度:0.9
组卷:2109引用:17难度:0.9 -
8.疫情期间,某快递公司推出无接触配送服务,第1周接到5万件订单,第2周到第3周订单量增长率是第1周到第2周订单量增长率的1.5倍,若第3周接到订单为7.8万件,设第1周到第2周的订单增长率为x,可列得方程为( )
组卷:31引用:4难度:0.8
三、解答题(共72分)
-
23.已知抛物线y=ax2+3x+
的对称轴是直线x=3,与x轴相交于A,B两点(点B在点A右侧),与y轴交于点C.72
(1)求抛物线的解析式和A,B两点的坐标;
(2)如图1,若点P是抛物线上B、C两点之间的一个动点(不与B、C重合),是否存在点P,使四边形PBOC的面积最大?若存在,求点P的坐标及四边形PBOC面积的最大值;若不存在,请说明理由;
(3)如图2,若点M是抛物线上任意一点,过点M作y轴的平行线,交直线BC于点N,当MN=3时,求点M的坐标. 组卷:210引用:4难度:0.3
组卷:210引用:4难度:0.3 -
24.我们不妨约定:对于某一自变量为x的函数,若当x=m时,其函数值也为m.则称点(m,m)为此函数的“不动点”,如:二次函数y=x2有两个“不动点”,坐标分别为(1,1)和(0,0).
(1)一次函数y=3x-1的“不动点”坐标为 .
(2)若抛物线L:y=ax2-2ax+2上只有一个“不动点”A.
①求抛物线L的解析式和这个“不动点”A的坐标;
②在平面直角坐标系xOy中,将抛物线L平移后,得到抛物线L':y=ax2-2ax+2+n(n≠0),抛物线L'与y轴交于点B,连接OA,AB,若抛物线L'的顶点落在△OAB内部(不含边界),求出n的取值范围.组卷:42引用:2难度:0.2


