2023年广东省汕头市金平区丰华学校中考数学二模试卷

一.选择题（共10小题，满分30分，每小题3分）

• 1．芝麻被称为“八谷之冠”，是世界上最古老的油料作物之一，它作为食品和药物，得到广泛的使用．经测算，一粒芝麻的质量约为0.00000201千克，将0.00000201用科学记数法表示为（　　）

  A．0.201×10-5

  B．2.01×10-6

  C．2.01×10-5

  D．20.1×10-4
  组卷：313引用：13难度：0.8

  解析

• 2．以下是回收、绿色包装、节水、低碳四个标志，其中为中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：611引用：23难度：0.9

  解析

• 3．在数轴上表示下列各数的点中，距离原点最近的是（　　）

  A．-1

  B．- 2

  C． 1 2

  D．4
  组卷：47引用：1难度：0.5

  解析

• 4．将两本相同的书进行叠放，得到如图所示的几何体，则它的主视图是（　　）

  A．

  B．

  C．

  D．
  组卷：484引用：13难度：0.8

  解析

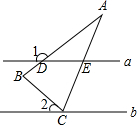• 5．如图，在△ABC中，AB=AC，∠A=30°，直线a∥b,顶点C在直线b上，直线a交AB于点D，交AC与点E，若∠1=145°，则∠2的度数是（　　）

  A．30°

  B．35°

  C．40°

  D．45°
  组卷：4051引用：40难度：0.5

  解析

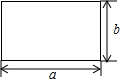• 6．如图，边长为a、b的长方形周长为20，面积为16，则a²b+ab²的值为（　　）

  A．80

  B．160

  C．320

  D．480
  组卷：1330引用：12难度：0.8

  解析

• 7．对于反比例函数y=-

  2023

  x

  ．下列说法不正确的是（　　）

  A．图象分布在二，四象限内

  B．图象经过点（1，-2023）

  C．当x＞0时，y随x的增大而增大

  D．若点A（x1，y1），B（x2，y2）都在函数的图象上，且x1＜x2时，则y1＜y2
  组卷：225引用：3难度：0.5

  解析

​三，解答题（共7小题，满分0分）

• 21．如图，抛物线y=-

  1

  2

  x²+bx+c过点A（3，2），且与直线y=-x+

  7

  2

  交于B、C两点，点B的坐标为（4，m）．
  
  （1）求抛物线的解析式；
  （2）点D为抛物线上位于直线BC上方的一点，过点D作DE⊥x轴交直线BC于点E，点P为对称轴上一动点，当线段DE的长度最大时，求PD+PA的最小值；
  （3）设点M为抛物线的顶点，在y轴上是否存在点Q，使∠AQM=45°？若存在，求点Q的坐标；若不存在，请说明理由．
  组卷：5785引用：26难度：0.1

  解析

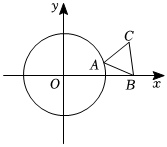• 22．如图，⊙O的半径为

  3

  ，正三角形ABC的顶点B的坐标为（2，0），顶点A在⊙O上运动．
  （1）当点A在x轴正半轴上时，求点C的坐标；
  （2）点A在运动过程中，是否存在直线AB与⊙O相切的位置关系？若存在，请直接写出点C的坐标；
  （3）设点A的横坐标为x,△ABC的面积为S，求S与x之间的函数关系式，并求出S的最大值与最小值．
  组卷：77引用：4难度：0.4

  解析