2023-2024学年福建省厦门外国语学校高二（上）段考数学试卷（10月份）

一、单项选择题：（本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）.

• 1．过A（1，-3），B（-2，0）两点的直线的倾斜角是（　　）

  A．45°

  B．60°

  C．120°

  D．135°
  组卷：447引用：14难度：0.7

  解析

• 2．如果存在三个不全为0的实数x、y、z,使得向量

  x

  a

  +

  y

  b

  +

  z

  c

  =

  0

  ，则关于

  a

  、

  b

  、

  c

  叙述正确的是（　　）

  A． a 、 b 、 c 两两互相垂直

  B． a 、 b 、 c 中只有两个向量互相垂直

  C． a 、 b 、 c 共面

  D． a 、 b 、 c 中有两个向量互相平行
  组卷：162引用：6难度：0.6

  解析

• 3．“a²=1”是“直线x+y=0和直线x-ay=0互相垂直”的（　　）

  A．充分而不必要条件	B．必要而不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：72引用：9难度：0.9

  解析

• 4．已知A（-2，0），B（4，a）两点到直线l：3x-4y+1=0的距离相等，则a=（　　）

  A．2

  B． 9 2

  C．2或-8

  D．2或 9 2
  组卷：1501引用：25难度：0.8

  解析

• 5．已知

  a

  ，

  b

  ，

  c

  是不共面的三个向量，则能构成空间的一个基底的一组向量是（　　）

  A．3 a ， a - b ， a +2 b	B．2 b ， b -2 a ， b +2 a
  C． a ，2 b ， b - c	D． c ， a + c ， a - c
  组卷：514引用：19难度：0.7

  解析

• 6．已知直线l：（m+2）x+（m-1）y+m-1=0，若直线l与连接A（1，-2）、B（2，1）两点的线段总有公共点，则直线l的倾斜角范围为（　　）

  A． [ - π 4 ， π 4 ]	B． [ 3 π 4 ， π ）
  C． [ π 4 ， 3 π 4 ]	D． [ 0 ， π 4 ] ∪ [ 3 π 4 ， π ）
  组卷：77引用：12难度：0.8

  解析

• 7．如图，圆柱的轴截面为矩形ABCD，点M，N分别在上、下底面圆上，

  ˆ

  NB

  =

  2

  ˆ

  AN

  ，

  ˆ

  CM

  =

  2

  ˆ

  MD

  ，AB=2，BC=3，则异面直线AM与CN所成角的余弦值为（　　）

  A． 3 30 10

  B． 3 4

  C． 3 5

  D． 3 30 20
  组卷：255引用：13难度：0.6

  解析

四、解答题：共70分.解答应写出文字说明，证明过程或演算步.

• 21．如图，在直三棱柱ABC-A₁B₁C₁中，∠BAC=60°，AC=AB=2，AA₁=3．M是AB的中点，P是BC₁与B₁C的交点，Q是上底面A₁B₁C₁的动点．
  （1）是否存在点Q，使得PQ∥平面A₁CM？若存在，请确定Q点的位置；若不存在，请说明理由；
  （2）在（1）的条件下，当PQ最短时，求平面PQM与平面A₁CM的夹角的余弦值．
  组卷：32引用：1难度：0.4

  解析

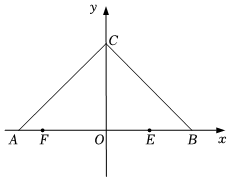• 22．已知△ABC的三个顶点分别为A（-2，0），B（2，0），C（0，2）．
  （1）若过P（1，2）的直线y=ax+b将△ABC分割为面积相等的两部分，求b的值；
  （2）一束光线从E（1，0）点出发射到BC上的D点，经BC反射后，再经AC反射到x轴上的F点，最后再经x轴反射，反射光线所在直线为l,证明直线l经过一定点，并求出此定点的坐标．
  组卷：145引用：2难度：0.5

  解析