【问题引领】
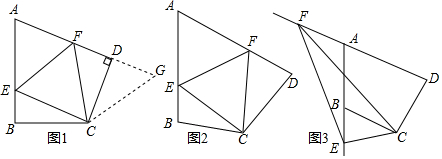
问题1：如图1，在四边形ABCD中，CB=CD，∠B=∠ADC=90°，∠BCD=120°．E，F分别是AB，AD上的点．且∠ECF=60°．探究图中线段BE，EF，FD之间的数量关系．
小王同学探究此问题的方法是，延长FD到点G．使DG=BE．连接CG，先证明△CBE≌△CDG，再证明△CEF≌△CGF．他得出的正确结论是 BE+FD=EFBE+FD=EF．
【探究思考】
问题2：如图2，若将问题1的条件改为：四边形ABCD中，CB=CD，∠ABC+∠ADC=180°，∠ECF=12∠BCD，问题1的结论是否仍然成立？请说明理由．
【拓展延伸】
问题3：如图3在问题2的条件下，若点E在AB的延长线上，点F在DA的延长线上，则问题2的结论是否仍然成立？若不成立，猜测此时线段BE、DF、EF之间存在什么样的等量关系？并说明理由．
1
2
【考点】三角形综合题．
【答案】BE+FD=EF
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/17 2:0:1组卷：1240引用：14难度：0.1
相似题
-
1．已知直角△ABC，∠BAC=90°，D是斜边BC的中点，E、F分别是AB、AC边上的点，且DE⊥DF，连接EF．
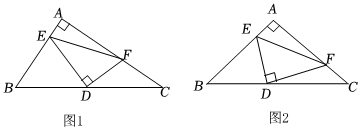
（1）如图1，求证：∠BED=∠AFD；
（2）如图1，求证：BE2+CF2=EF2；
（3）如图2，当∠ABC=45°，若BE=4，CF=3，求△DEF的面积．发布：2024/12/23 14:0:1组卷：216引用：3难度：0.2 -
2．一副三角板如图1摆放，∠C=∠DFE=90°，∠B=30°，∠E=45°，点F在BC上，点A在DF上，且AF平分∠CAB，现将三角板DFE绕点F顺时针旋转（当点D落在射线FB上时停止旋转）．
（1）当∠AFD=°时，DF∥AC；当∠AFD=°时，DF⊥AB；
（2）在旋转过程中，DF与AB的交点记为P，如图2，若△AFP有两个内角相等，求∠APD的度数；
（3）当边DE与边AB、BC分别交于点M、N时，如图3，若∠AFM=2∠BMN，比较∠FMN与∠FNM的大小，并说明理由．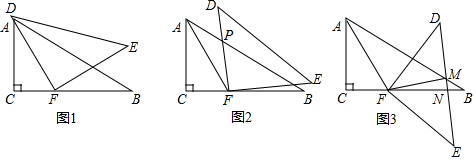
发布：2024/12/23 18:30:1组卷：1754引用：10难度：0.1 -
3．已知A（0，4），B（-4，0），D（9，4），C（12，0），动点P从点A出发，在线段AD上，以每秒1个单位的速度向点D运动：动点Q从点C出发，在线段BC上，以每秒2个单位的速度向点B运动，点P、Q同时出发，当其中一个点到达终点时，另一个点随之停止运动，设运动时间为t（秒）．
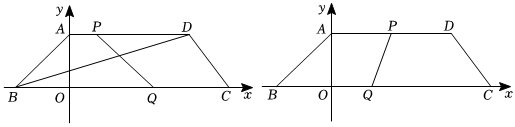
（1）当t=秒时，PQ平分线段BD；
（2）当t=秒时，PQ⊥x轴；
（3）当时，求t的值．∠PQC=12∠D发布：2024/12/23 15:0:1组卷：184引用：3难度：0.1
