探究与发现：如图①，在Rt△ABC中，∠BAC=90°，AB=AC，点D在底边BC上，AE=AD，连接DE．
（1）当∠BAD=60°时，求∠CDE的度数；
（2）当点D在BC（点B、C除外）上运动时，试猜想并探究∠BAD与∠CDE的数量关系；
（3）深入探究：若∠BAC≠90°，试就图②探究∠BAD与∠CDE的数量关系．

【答案】见试题解答内容

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

发布：2024/6/27 10:35:59组卷：3941引用：10难度：0.3

相似题

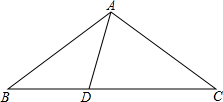1．如图，△ABC中，AB=AC=CD，BD=AD，求△ABC中各角的度数．
发布：2025/1/20 8:0:1组卷：874引用：16难度：0.5
解析
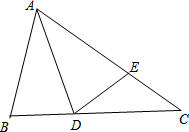2．如图，△ABC中，AB=AD=AE，DE=EC，∠DAB=30°，求∠C的度数．
发布：2025/1/20 8:0:1组卷：537引用：2难度：0.1
解析
3．（1）计算：|1-
2
|-
3
-
1
8
+
（
-
2
）
2
；
（2）分解因式：（2a+b）²-8ab；
（3）先化简，再求值：（a+b）（a-b）+（a+b）²-2a²，其中a=3，b=-
1
3
；
（4）如图，在△ABC中，AC=AD=BD，∠DAC=4∠B，试求∠B的度数．
发布：2025/1/24 8:0:2组卷：39引用：1难度：0.5
解析

1．如图，△ABC中，AB=AC=CD，BD=AD，求△ABC中各角的度数．