某公司分别在A，B两城生产同种产品，共100件．A城生产产品的总成本y（万元）与产品数量x（件）之间具有函数关系y=x2+20x+100，B城生产产品的每件成本为60万元．
（1）当A城生产多少件产品时，A，B两城生产这批产品成本的和最小，最小值是多少？
（2）从A城把该产品运往C，D两地的费用分别为1万元/件和3万元/件；从B城把该产品运往C，D两地的费用分别为1万元/件和2万元/件．C地需要90件，D地需要10件，在（1）的条件下，怎样调运可使A，B两城运费的和最小？
【考点】二次函数的应用．
【答案】（1）当A城生产20件产品时，A，B两城生产这批产品成本的和最小，最小值是5700元；
（2）从A城把该产品运往C地的产品数量为20件，则从A城把该产品运往D地的产品数量为0件；从B城把该产品运往C地的产品数量为70件，则从B城把该产品运往D地的产品数量为10件时，可使A，B两城运费的和最小．
（2）从A城把该产品运往C地的产品数量为20件，则从A城把该产品运往D地的产品数量为0件；从B城把该产品运往C地的产品数量为70件，则从B城把该产品运往D地的产品数量为10件时，可使A，B两城运费的和最小．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/15 8:0:8组卷：81引用：2难度：0.4
相似题
-
1．2022年2月8日北京冬奥会中自由滑雪空中技巧项目备受大家关注，中国优秀运动员沿跳台斜坡AB加速加速至B处腾空而起，沿抛物线BEF运动，在空中完成翻滚动作，着陆在跳台的背面着陆坡DC．建立如图所示的平面直角坐标系，BD∥x轴，C在x轴上，B在y轴上，已知跳台的背面DC近似是抛物线y=a（x-7）2（1≤x≤7）的一部分，D点的坐标为（1，6），抛物线BEF的表达式为y=b（x-2）2+k.
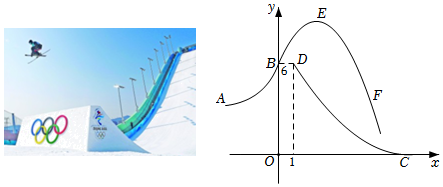
（1）当k=10时，求a、b的值；
（2）在（1）的条件下，运动员在离x轴3.75m处完成动作并调整好身姿，求此时他距DC的竖直距离（竖直距离指的是运动员所在位置的点向x轴的垂线与DC的交点之间线段的长）；
（3）若运动员着落点与B之间的水平距离需要在不大于7m的位置（即着落点的横坐标x满足x≤7且b＜0，），求b的取值范围．发布：2024/12/23 13:30:1组卷：356引用：4难度：0.4 -
2．如图1，某公园在入园处搭建了一道“气球拱门”，拱门两端落在地面上．若将拱门看作抛物线的一部分，建立如图2所示的平面直角坐标系．拱门上的点距地面的竖直高度y（单位：m）与水平距离x（单位：m）近似满足函数关系y=a（x-h）2+k（a＜0）．
（1）拱门上的点的水平距离x与竖直高度y的几组数据如下：
根据上述数据，直接写出“门高”（拱门的最高点到地面的距离），并求出拱门上的点满足的函数关系y=a（x-h）2+k（a＜0）．水平距离x/m 2 3 6 8 10 12 竖直高度y/m 4 5.4 7.2 6.4 4 0
（2）一段时间后，公园重新维修拱门．新拱门上的点距地面的竖直高度y（单位：m）与水平距离x（单位：m）近似满足函数关系y=-0.288（x-5）2+7.2，若记“原拱门”的跨度（跨度为拱门底部两个端点间的距离）为d1，“新拱门”的跨度为d2，则d1d2（填“＞”“=”或“＜”）．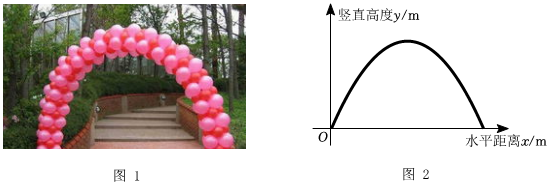
发布：2024/12/23 11:30:2组卷：581引用：6难度：0.5 -
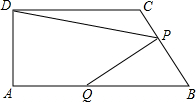3．如图，已知梯形ABCD中，DC∥AB，∠A=90°，∠B=60°，AD=3，AB=，DC=53，P是BC边上一点（P与B不重合），过点P作PQ⊥BC交AB于Q，设PB=x,四边形AQPD的面积为y.43
（1）求y与x的函数关系式；
（2）当x为何值时，y有最大值或最小值？其值等于多少？发布：2025/1/21 8:0:1组卷：31引用：1难度：0.5
