我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b2展开式中的系数等等.
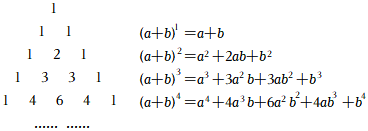
(1)根据上面的规律,则(a+b)5的展开式为(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5.
(2)(a+b)n的展开式共有 (n+1)(n+1)项,系数和为 2n2n.
(3)利用上面的规律计算:25-5×24+10×23-10×22+5×2-1.
(4)运用:若今天是星期二,经过86天后是星期 三三.
【答案】(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;(n+1);2n;三
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/6/27 10:35:59组卷:287引用:1难度:0.6
相似题
-
1.已知a-b=1,a2+b2=13,求下列代数式的值:
(1)ab;
(2)a2-b2-8.发布:2025/6/16 0:0:1组卷:2825引用:5难度:0.7 -
2.我国南宋数学家杨辉用三角形解释二项和的乘方规律,称之为“杨辉三角”.这个三角形给出了(a+b)n(n=1,2,3,4…)的展开式的系数规律(按a的次数由大到小的顺序).
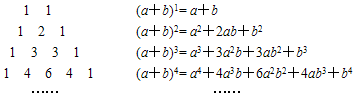
请依据规律,写出展开式中含x2018项的系数是 .(x-2x)2020发布:2025/6/15 18:30:1组卷:380引用:6难度:0.7 -
3.(1)已知m+n=4,mn=2,求m2+n2的值;
(2)已知am=3,an=5,求a3m-2n的值.发布:2025/6/15 18:30:1组卷:2288引用:8难度:0.7


