乘法公式的探究及应用．
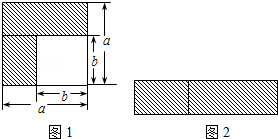（1）如图1，可以求出阴影部分的面积是 a2-b2a2-b2（写成两数平方差的形式）；
（2）如图2，若将阴影部分裁剪下来，重新拼成一个长方形，它的宽是 a-ba-b，长是 a+ba+b，面积是 （a+b）（a-b）（a+b）（a-b）（写成多项式乘法的形式）；
（3）比较左、右两图的阴影部分面积，可以得到乘法公式 （a+b）（a-b）=a2-b2（a+b）（a-b）=a2-b2（用式子表达）；
（4）运用你所得到的公式，计算下题：103×97．
【考点】平方差公式的几何背景．
【答案】a2-b2；a-b；a+b；（a+b）（a-b）；（a+b）（a-b）=a2-b2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/14 8:0:9组卷：62引用：2难度：0.8
相似题
-
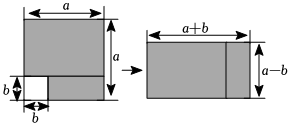1．如图，从边长为a的大正方形纸板的边上挖去一个边长为b的小正方形纸板后，沿着小正方形的缺口，将其裁成两个长方形，然后拼成一个长方形．那么通过计算两个图形阴影部分的面积，可以验证成立的公式为（ ）发布：2024/12/23 8:30:2组卷：234引用：4难度：0.8 -
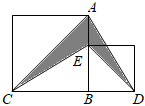2．如图，大正方形与小正方形的面积之差是80，则阴影部分的面积是（ ）发布：2024/12/23 20:0:2组卷：845引用：5难度：0.7 -
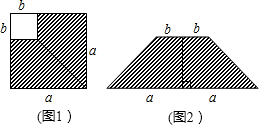3．如图1，在边长为a的正方形中剪去一个边长为b的小正方形（a＞b），把剩下部分拼成一个梯形（如图2），利用这两幅图形面积，可以验证的公式是（ ）发布：2024/12/23 8:30:2组卷：5238引用：46难度：0.9
