数学活动课上,老师准备了若干张如图1所示的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b、宽为a的长方形.现在用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2所示的大正方形.观察图形并解答下列问题.
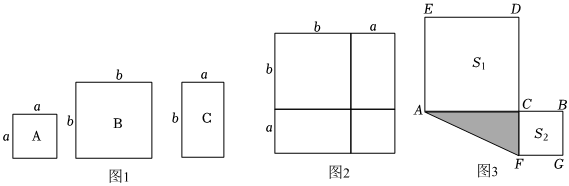
(1)由图1到图2的过程可得到的因式分解等式为(用含a,b的代数式表示);
(2)小敏用图1中的A、B、C三种纸片拼出一个面积为 (3a+b)(a+2b) 的大长方形,求需要A、B、C三种纸片各多少张;
(3)如图3,C为线段AB上的动点,分别以AC,BC为边在AB的两侧作正方形ACDE和正方形BCFG.若AB=5,记正方形ACDE和正方形BCFG的面积分别为 S1S2,且 S1+S2=17,利用(1)中的结论求图中三角形ACF的面积.
【答案】(1)a2+2ab+b2=(a+b)2;
(2)需要A种纸片3张,B种纸片2张,C种纸片7张;
(3)2.
(2)需要A种纸片3张,B种纸片2张,C种纸片7张;
(3)2.
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/6/4 8:0:5组卷:320引用:1难度:0.5
相似题
-
1.阅读下列题目的解题过程:
已知a、b、c为△ABC的三边长,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状.
解:∵a2c2-b2c2=a4-b4(A)
∴c2(a2-b2)=(a2+b2)(a2-b2) (B)
∴c2=a2+b2(C)
∴△ABC是直角三角形
问:(1)上述解题过程,从哪一步开始出现错误?请写出该步的代号:;
(2)错误的原因为:;
(3)本题正确的结论为:.发布:2024/12/23 18:0:1组卷:2622引用:25难度:0.6 -
2.若a是整数,则a2+a一定能被下列哪个数整除( )
发布:2024/12/24 6:30:3组卷:417引用:7难度:0.6 -
3.阅读理解:
能被7(或11或13)整除的特征:如果一个自然数末三位所表示的数与末三位以前的数字所表示的数之差(大数减小数)是7(或11或13)的倍数,则这个数就能被7(或11或13)整除.
如:456533,533-456=77,77是7的11倍,所以,456533能被7整除.又如:345548214,345548-214=345334,345-334=11,11是11的1倍,所以,345548214能被11整除.
(1)用材料中的方法验证67822615是7的倍数(写明验证过程);
(2)若对任意一个七位数,末三位所表示的数与末三位以前的数字所表示的数之差(大数减小数)是11的倍数,证明这个七位数一定能被11整除.发布:2025/1/5 8:0:1组卷:134引用:3难度:0.4


