2022-2023学年北京二中朝阳学校八年级（上）月考数学试卷（11月份）

一、选择题

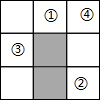• 1．如图是3×3的正方形网格，其中已有2个小方格涂成了黑色．现在要从编号为①‒④的小方格中选出1个也涂成黑色，使黑色部分依然是轴对称图形，不能选择的是（　　）

  A．①

  B．②

  C．③

  D．④
  组卷：733引用：8难度：0.7

  解析

• 2．下列等式中，从左到右的变形是因式分解的是（　　）

  A．m（a+b）=ma+mb	B．3x2-3x+1=3x（x-1）+1
  C．x2+3x+2=（x+1）（x+2）	D．（a+2）2=a2+4a+4
  组卷：359引用：5难度：0.7

  解析

• 3．下列各式计算正确的是（　　）

  A． a + b a + c = b c	B． 1 - a a - 2 =- a - 1 a - 2
  C．（ 2 y x ）3= 6 y 3 x 3	D． x 6 x 3 =x2
  组卷：184引用：1难度：0.7

  解析

• 4．分式

  1

  2

  a

  2

  b

  与

  1

  a

  b

  2

  的最简公分母是（　　）

  A．ab

  B．2a2b2

  C．a2b2

  D．2a3b3
  组卷：984引用：10难度：0.9

  解析

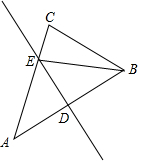• 5．如图，△ABC中，∠A=40°，AB的垂直平分线分别交AB，AC于点D，E，连接BE，则∠BEC的大小为（　　）

  A．40°

  B．50°

  C．80°

  D．100°
  组卷：2180引用：21难度：0.7

  解析

• 6．已知△ABC，两个完全一样的三角板如图摆放，它们的一组对应直角边分别在AB，AC上，且这组对应边所对的顶点重合于点M，点M一定在（　　）

  A．∠A的平分线上	B．AC边的高上
  C．BC边的垂直平分线上	D．AB边的中线上
  组卷：2857引用：38难度：0.8

  解析

• 7．对于任意的实数x,总有意义的分式是（　　）

  A． x - 5 x 2 - 1

  B． x - 3 x 2 + 1

  C． x 2 + 1 8 x

  D． 2 x - 1
  组卷：761引用：11难度：0.9

  解析

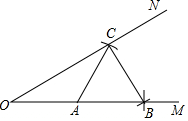• 8．如图，已知∠MON及其边上一点A．以点A为圆心，AO长为半径画弧，分别交OM，ON于点B和C，再以点C为圆心，AC长为半径画弧，恰好经过点B．错误的结论是（　　）

  A．S△AOC=S△ABC	B．∠OCB=90°
  C．∠MON=30°	D．OC=2BC
  组卷：837引用：14难度：0.7

  解析

三、解答题

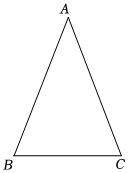• 23．老师给同学们布置了一个在平面内找一点，使该点到等腰三角形的三个顶点的距离相等”的尺规作图任务：
  下面是小聪同学设计的尺规作图过程：
  已知：如图，△ABC中，AB=AC．
  求作：一点P，使得PA=PB=PC．
  作法：
  ①作∠BAC的平分线AM交BC于点D；
  ②作边AB的垂直平分线EF，EF与AM相交于点P；
  ③连接PB，PC．
  所以，点P就是所求作的点
  根据小聪同学设计的尺规作图过程，
  （1）使用直尺和圆规，补全图形．（保留作图痕迹）
  （2）完成下面的证明．
  证明：∵AB=AC，AM平分∠BAC交BC于点D，
  ∴AD是BC的垂直平分线：（

  ）（填推理依据）
  ∴PB=PC．
  ∵EF垂直平分AB，交AM于点P，
  ∴PA=PB：（

  ）（填推理依据）
  ∴PA=PB=PC．
  （3）过点D作DG⊥AB，DH⊥AC，垂足分别为G，H．
  ∵AD平分∠BAC，
  ∴

  =

  （

  ）（填推理的依据）．
  组卷：58引用：2难度：0.5

  解析

• 24．已知：△ABC是等边三角形，D是直线BC上一动点，连接AD，在线段AD的右侧作射线DP且使∠ADP=30°，作点A关于射线DP的对称点E，连接DE、CE．
  
  （1）当点D在线段BC上运动时，
  ①依题意将图1补全；
  ②请用等式表示线段AB、CE、CD之间的数量关系，并证明；
  （2）当点D在直线BC上运动时，请直接写出AB、CE、CD之间的数量关系，不需证明．
  组卷：743引用：7难度：0.4

  解析