2022-2023学年河南省驻马店市汝南县七年级(下)期中数学试卷
发布:2024/7/5 8:0:9
一、选择题(每小题3分,共30分)
-
1.如图所示的四个图形中,∠1和∠2一定相等的是( )
组卷:171引用:3难度:0.9 -
 2.近段时间,以熊猫为原型的2022北京冬奥会吉祥物“冰墩墩”成了全网“顶流”.如图,通过平移如图吉祥物“冰墩墩”可以得到的图形是( )组卷:859引用:33难度:0.9
2.近段时间,以熊猫为原型的2022北京冬奥会吉祥物“冰墩墩”成了全网“顶流”.如图,通过平移如图吉祥物“冰墩墩”可以得到的图形是( )组卷:859引用:33难度:0.9 -
3.下列式子正确的是( )
组卷:103引用:2难度:0.9 -
4.在平面直角坐标系中,下面的点在第一象限的是( )
组卷:127引用:13难度:0.9 -
5.下列命题中,是真命题的是( )
组卷:179引用:5难度:0.6 -
6.在平面直角坐标系中,将点A(-1,-7)向右平移3个单位长度,再向上平移4个单位长度后与点B重合,则点B的坐标是( )
组卷:48引用:2难度:0.5 -
 7.如图,点E在AC的延长线上,下列条件不能判断AC∥BD的是( )组卷:916引用:30难度:0.9
7.如图,点E在AC的延长线上,下列条件不能判断AC∥BD的是( )组卷:916引用:30难度:0.9
三、解答题(共70分)
-
22.本学期我们在第六章《实数》中学习了平方根和立方根.如表是平方根和立方根的部分内容.通过类比平方根和立方根的有关内容可以了解有关四次方根的知识请仔细阅读下表并解决下列问题:
(1)类比平方根和立方根的定义,给四次方根下定义:平方根 立方根 定义 一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根.这就是说,如果x2=a,那么x叫做a的平方根. 一般地,如果一个数的立方等于a,那么这个数叫做a的立方根或三次方根.这就是说,如果x3=a,那么x叫做a的立方根. 运算 求一个数a的平方根的运算,叫做开平方.开平方与平方互为逆运算. 求一个数a的立方根的运算,叫做开立方.开立方与立方互为逆运算. 特征 正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根. 正数的立方根是正数;
0的立方根是0;
负数的立方根是负数.表示与读法 正数a的平方根可以用“± ”表示,读作“正负根号a”.a一个数a的立方根可以用“ ”表示,读作“三次根号a”.3a
一般地,,那么x叫作a的四次方根.
(2)思考与归纳
求一个数a的四次方根的运算叫做开四次方.开四次方和四次方互为逆运算.
①探究:
81的四次方根是 ;
0的四次方根是 ;
-4 (填“有”或“没有”)四次方根.
②归纳:
根据上述①中情况,类比平方根和立方根的特征,归纳四次方根的特征:;
③总结:
我们归纳四次方根的特征时,分了正数、0、负数三类进行研究,这种思想叫 ;
四次方根的特征是由81,,0等这几个特殊数的四次方根的特征归纳出来的,这种思想叫 (填正确选项的代码).1681
A.类比思想
B.分类讨论思想
C.由一般到特殊的思想
D.由特殊到一般的思想
(3)巩固与应用
①±= (将结果直接填到横线上).4256
②比较大小:3(填“>”或“=”或“<”).416组卷:132引用:1难度:0.5 -
23.【问题背景】
同学们,我们一起观察小猪的猪蹄,你会发现一个我们熟悉的几何图形,我们就把这个图形象的称为“猪蹄模型”,猪蹄模型中蕴含着角的数量关系.
(1)如图1,AB∥CD,E为AB,CD之间一点,连接BE,DE,得到∠BED.试探究∠BED与∠B、∠D之间的数量关系,并说明理由.
(2)【类比探究】请你利用上述“猪蹄模型”得到的结论或解题方法,完成下面的问题:
如图2,已知MN∥PQ,CD∥AB,点E在PQ上,∠ECN=∠CAB,请你说明∠ABP+∠DCE=∠CAB;(把下面的解答补充完整)
解:因为CD∥AB
所以∠CAB+=180°( )
因为∠ECM+∠ECN=180°( )
又因为∠ECN=∠CAB
所以∠=∠( )
即∠MCA+∠ACE=∠DCE+∠ACE
所以∠MCA=∠DCE
由(1)知∠MCA+∠ABP=∠CAB
∴∠ABP+∠DCE=∠CAB
(3)【拓展延伸】如图3,BF平分∠ABP,CG平分∠ACN,AF∥CG.若∠CAB=68°,请直接写出∠AFB的度数为 .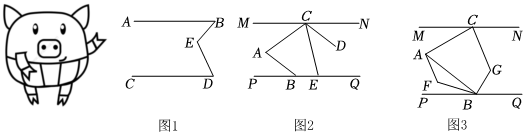 组卷:2402引用:8难度:0.3
组卷:2402引用:8难度:0.3


