2022-2023学年山东省淄博一中高二（下）第二次月考数学试卷
发布：2024/7/6 8:0:9
一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.
-
1．在等比数列{an}中，有a3a15=8a9，数列{bn}是等差数列，且b9=a9，则b7+b11等于（ ）
组卷：145引用：4难度：0.7 -
2．函数f（x）=2lnx-x2的单调递增区间为（ ）
组卷：38引用：13难度：0.7 -
3．将甲、乙等5名交警分配到三个不同路口疏导交通，每个路口至少一人，且甲、乙在同一路口的分配方案共有（ ）
组卷：404引用：8难度：0.9 -
4．已知数列{an}的前n项和Sn=3an-2，设bn=lo
an，则g32+1b2b3+⋯+1b3b4=（ ）1b2022b2023组卷：161引用：4难度：0.5 -
5．据美国的一份资料报道，在美国总的来说患肺癌的概率约为0.1%，在人群中有20%是吸烟者，他们患肺癌的概率约为0.4%，则不吸烟患肺癌的概率为（ ）
组卷：696引用：5难度：0.7 -
6．一台仪器每启动一次都会随机地出现一个3位的二进制数A=a1a2a3，其中A的各位数中，ak（k=1，2，3）出现0的概率为
，出现1的概率为13．若启动一次出现的二进制数为A=100，则称这次试验成功．若成功一次得2分，失败一次得-1分，则81次这样的独立重复试验的总得分Y的数学期望为（ ）23组卷：67引用：2难度：0.5 -
7．下列不等式中不成立的是（ ）
组卷：53引用：3难度：0.6
四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.
-
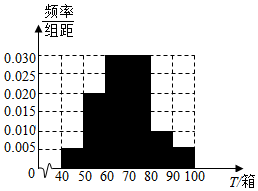21．某物流公司专营从甲地到乙地的货运业务（货物全部用统一规格的包装箱包装），现统计了最近100天内每天可配送的货物量，按照可配送货物量T（单位：箱）分成了以下几组：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]，并绘制了如图所示的频率分布直方图（同一组数据用该组数据的区间中点值作代表，将频率视为概率）．
（Ⅰ）该物流公司负责人决定用分层抽样的方法从前3组中随机抽出11天的数据来分析可配送货物量少的原因，并从这11天的数据中再抽出3天的数据进行财务分析，求这3天的数据中至少有2天的数据来自[50，60）这一组的概率．
（Ⅱ）由频率分布直方图可以认为，该物流公司每日的可配送货物量T（单位：箱）服从正态分布N（μ，14.42），其中μ近似为样本平均数．
（ⅰ）试利用该正态分布，估计该物流公司2000天内日货物配送量在区间（54.1，97.3）内的天数（结果保留整数）．
（ⅱ）该物流公司负责人根据每日的可配送货物量为公司装卸货物的员工制定了两种不同的工作奖励方案．
方案一：直接发放奖金，按每日的可配送货物量划分为以下三级：T＜60时，奖励50元；60≤T＜80，奖励80元；T≥80时，奖励120元．
方案二：利用抽奖的方式获得奖金，其中每日的可配送货物量不低于μ时有两次抽奖机会，每日的可配送货物量低于μ时只有一次抽奖机会，每次抽奖的奖金及对应的概率分别为
小张恰好为该公司装卸货物的一名员工，试从数学期望的角度分析，小张选择哪种奖励方案对他更有利？奖金 50 100 概率 4515
附：若Z～N（μ，σ2），则P（μ-σ＜Z＜μ+σ）≈0.6827，P（μ-2σ＜Z＜μ+2σ）≈0.9545．组卷：378引用：5难度：0.5 -
22．已知函数f（x）=
．alnxx（a∈R），g（x）=ex-1x
（1）讨论函数f（x）的单调性；
（2）令h（x）=f（x）-g（x），当a=1时，求h（x）的最大值．组卷：41引用：3难度：0.3
